Suponhamos o conjunto {1, 3, 4}. Mudando a ordem dos elementos obtemos os conjuntos {1, 4, 3}, {3, 1, 4}, {3, 4, 1}, {4, 1, 3} e {4, 3, 1} que são todos iguais. Concluímos que a ordem dos elementos não influi. Um agrupamento com esta característica é chamado combinação simples de n elementos dados, tomados p a p.

Exemplo 1:
Se considerarmos o conjunto B ={A,B,C,D} formados por 4 pontos não colineares (que não pertence a mesma reta), qual a quantidade de triângulos que podemos formar?
Nesse problema iremos formar agrupamentos. Nesse caso o agrupamento é formar triângulos utilizando 4 pontos não colineares. Se destacarmos dois agrupamentos formados teremos: ABC e BCA, esses são triângulos formados com os mesmos pontos, mas em ordens diferentes que torna os triângulos iguais. Portanto, os agrupamentos formados nesse exercício são combinações.
As combinações simples podem ser consideradas um tipo particular de arranjo simples, pois os agrupamentos formados nos arranjos são diferenciados pela ordem e pela natureza dos seus elementos. A combinação simples são esses arranjos diferenciados apenas pela natureza de seus elementos.
Considerando o exemplo acima veja todas as possibilidades de triângulos formados com os quatro pontos não colineares:
ABC, BAC, CAB, DAB
ABD, BAD, CAD, DAC
ACB, BCA, CBA, DBA
ACD, BCD, CBD, DBC
ADB, BDA, CDA, DCA
ADC, BDC, CDB, DCB
Percebemos que há vários agrupamentos que se diferem pela ordem de seus elementos, esses representam o mesmo triângulo, por isso que consideramos esse exercício como sendo uma combinação simples, assim a quantidade de combinações simples que os 4 pontos não colineares (A,B,C,D), tomados 3 a 3 irão formar será 4, pois os seus agrupamentos se diferem pela natureza de seus elementos e não pela ordem.
Para encontrar essa quantidade de agrupamentos formados em uma combinação simples utilizamos a seguinte fórmula:
Cn,p = n!
p! (n – p)
n é a quantidade de elementos de um conjunto
p é um número natural menor ou igual a n, que representa a quantidade de elementos que irão formar os agrupamentos.
Substituindo os dados acima na fórmula teremos:
n = 4
p = 3
C4,3 = 4! 3! (4-3)!
C4,3 = 4 . 3!
3! . 1
C4,3 = 4
Exemplo 2:
Numa firma de engenharia trabalham 4 engenheiros. Dois deverão ir para o exterior a fim de fazer cursos de aperfeiçoamento. De quantos modos a escolha poderá ser feita?
Representaremos por E1, E2, E3 e E4, os 4 engenheiros.
Vamos determinar todos os subconjuntos de 2 elementos do conjunto de 4 elementos {E1, E2, E3, E4}.
A ordem em que os elementos aparecem nesses subconjuntos não importa, pois E1 e E2, por exemplo, é a mesma que E2 e E1.
Assim, os subconjuntos de 2 elementos são:
{E1, E2}, {E1, E3}, {E1, E4}, {E2, E3}, {E2, E4}, {E3, E4}. Logo, existem 6 modos diferentes de escolher 2 engenheiros de um total de 4.
Assim, os subconjuntos chamamos de combinação simples de 4 elementos tomados 2 a 2, e escrevemos C4, 2.
Usando a fórmula acima, temos:

Exemplo 3: Ane, Elisa, Rosana, Felipe e Gustavo formam uma equipe. Dois deles precisam representar a equipe em uma apresentação. Quais e quantas são as possibilidades?
Representamos cada pessoa por uma letra
A: Ane;
E: Elisa;
R: Rosana;
F: Felipe;
G: Gustavo.
Precisamos determinar todos os subconjuntos de 2 elementos do conjunto de 5 elementos {A,E,R,F,G}. A ordem em que os elementos aparecem nos subconjuntos não importa, pois Ane-Elisa, por exemplo, é a mesma dupla que Elisa-Ane.
Então, os subconjuntos de 2 elementos são?
{A,E},{A,R},{A,F},{A,G},{E,R}{E,F},{E,G},{R,F},{R,G}{F,G}.
Chamamos estes subconjuntos de combinação simples de 5 elementos tomados com 2 a 2. Escrevemos C5,2 .
Onde C5, 2 representa a fórmula das combinações simples:
Substituindo na fórmula


Preste atenção nesta próxima propriedade das combinações.
Propriedade importante das combinações:
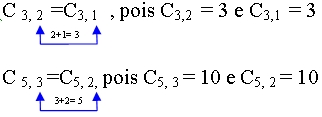
De modo geral temos que:
Cn, p = Cn, n-p
Combinação com repetição
Combinação com repetição: Neste tipo de combinação,todos os elementos podem aparecer repetidos em cada grupo até p vezes.
Fórmula: Cr(m,p)=C(m+p-1,p)
Cálculo para o exemplo: Cr(4,2)=C(4+2-1,2)=C(5,2)=5!/[2!3!]=10
Exemplo: Seja C={A,B,C,D}, m=4 e p=2. As combinações com repetição desses 4 elementos tomados 2 a 2 são 10 grupos que têm todas as repetições possíveis de elementos em grupos de 2 elementos não podendo aparecer o mesmo grupo com a ordem trocada. De um modo geral neste caso, todos os agrupamentos com 2 elementos formam um conjunto com 16 elementos:
Cr={AA,AB,AC,AD,BA,BB,BC,BD,CA,CB,CC,CD,DA,DB,DC,DD}
mas para obter as combinações com repetição, deveremos excluir deste conjunto os 6 grupos que já apareceram antes, pois AB=BA, AC=CA, AD=DA, BC=CB, BD=DB e CD=DC, assim as combinações com repetição dos elementos de C tomados 2 a 2, são:
Cr={AA,AB,AC,AD,BB,BC,BD,CC,CD,DD}
Fontes: http://www.mundoeducacao.com.br/matematica/combinacao-simples.htm
http://matematica.com.br/
http://matematica-na-veia.blogspot.com.br/
Questões resolvidas sobre combinação simples
1) Uma prova consta de 6 questões, das quais o aluno deve resolver 3. De quantas formas ele poderá escolher as 3 questões?
Solução:
Quer-se agrupar 3 elementos, dentre os 6 existentes.
Perceba que a ordem em que os elementos aparecerão não será importante, uma vez que, ao resolver a 1ª , a 2ª e a 3ª questão é o mesmo que resolver a 2ª , a 3º e a 1ª, portanto é um problema de combinação.
Logo, um aluno pode escolher suas 3 questões de 20 maneiras diferentes.

Faça você os arranjos, e depois verifique como foi feito nos exemplos anteriores, que esta afirmação é verdadeira.
2) Um time de futebol é composto de 11 jogadores, sendo 1 goleiro, 4 zagueiros, 4 meio campistas e 2 atacantes. Considerando-se que o técnico dispõe de 3 goleiros, 8 zagueiros, 10 meio campistas e 6 atacantes, determine o número de maneiras possíveis que esse time pode ser formado.
Solução:
Goleiros: C3,1
Zagueiros: C8,4
Meio campistas: C10,4
Atacantes: C6,2
Zagueiros: C8,4
Meio campistas: C10,4
Atacantes: C6,2

C3,1 * C8,4 * C10,4 * C6,2 = 3 * 70 * 210 * 15 = 661 500 maneiras de o time ser formado
Solução:
Comissão de alunas será dada por: C11,4
Comissão de alunos será composta por: C7,3
Comissão de alunos será composta por: C7,3

O número de comissões, respeitando a condição imposta, será de 11 550.
Solução:
Dos 12 jogadores, 2 são titulares absolutos, então teremos 10 jogadores disputando 3 vagas. Portanto, temos a seguinte combinação: C10, 3.

O treinador poderá formar 120 equipes.
5) Quantas saladas de frutas diferentes podemos formar com 5 frutas, se possuo 8 frutas distintas?
Solução:
 saladas
saladas
6) De quantos modos podemos escolher 2 objetos em um grupo de 6 objetos distintos?
Solução:
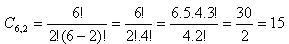 modos.
modos.
7) Uma escola tem 9 professores de matemática. Quatro deles deverão representar a escola em um congresso. Quantos grupos de 4 são possíveis? Os agrupamentos são combinações simples, pois um deles se distingue do outro somente quando apresenta pelo menos uma pessoa diferente. I nvertendo a ordem dos elementos, não alteramos o grupo.
Calculamos inicialmente os arranjos simples formados por 4 entre os 9 professores de matemática (mi):
Solução:

8) Uma associação tem uma diretoria formada por 10 pessoas das quais, 6 são homens, e 4 são mulheres. De quantas maneiras podemos formar uma comissão dessa diretoria que tenha 3 homens e 2 mulheres?
Solução:
C6, 3 .C4, 2 = 6.20 = 120 maneiras de formar uma comissão com 3 homens e 2 mulheres.
Solução:
A= {a1, a2, a3,..., a15} Onde, n=15 e p= 6, pois temos que uma equipe de vôlei é formada por 6 atletas. Logo, colocando os dados na fórmula de combinações simples, temos:
10) Uma urna contém 5 bolas azuis e 4 bolas vermelhas. De quantas maneiras podemos selecionar:
a) 3 bolas?
b) 3 bolas azuis e 2 vermelhas?
c) 3 bolas vermelhas e 2 azuis?
a) Observe que temos um total de 5 +4= 9 bolas dentro da urna.
Logo temos n=9 e pbolas = 3 . Logo, para n=9 e pbolas =3 temos:
b) Observe que temos um total de 5 +4= 9 bolas dentro da urna.
Logo temos n=9, pazuis = 3 e pvermelhas = 2. Logo, para n=9, pazuis= 3 e pvermelhas = 2 temos:
Das 5 bolas azuis arranjamos três a três, e das 4 bolas vermelhas arranjamos duas a duas. Então ao montar temos a seguinte multiplicação:
C5, 3 . C4, 2 . Fazendo
Logo, multiplicando os resultados encontrados nas combinações acima, temos:
6.10=60 maneiras diferentes.
c) Observe que temos um total de 5 +4= 9 bolas dentro da urna.
Logo temos n=9, pazuis = 2 e pvermelhas = 3. Logo, para n=9, pazuis = 2 e pvermelhas = 3 temos:
Das 5 bolas azuis arranjamos duas a duas, e das 4 bolas vermelhas arranjamos três a três. Então ao montar temos a seguinte multiplicação:
C5, 2 . C4, 3
4.10=40 maneiras diferentes.
O triângulo fica determinado por 3 pontos não-alinhados, não importando a ordem deles.

solução:
Veja no desenho que o triângulo ACD é determinado sem considerar a ordem deles (pode ser ADC, CDA, ...).
12) No congresso Nacional, uma comissão de 5 membros será formada a partir de 8 senadores e 6 deputados, sendo que pelo menos um deputado deverá pertencer à comissão. Calcule o número de comissões que poderão ser formadas.
solução:
A comissão poderá ser formada por:
4 senadores e 1 deputado: C8,4 . C6,1 = 70 . 6 = 420
3 senadores e 2 deputados: C8,3 . C6,2 = 56 . 15 = 840
2 senadores e 3 deputados: C8,2 . C6,3 = 28 . 20 = 560
1 senador e 4 deputados: C8,1 . C6,4 = 8 . 15 = 120
5 deputados: C6,5 = 6
____
total = 1.946
Logo, poderão ser formadas 1.946 comissões.
13) (PUC-RIO 2008) O número total de maneiras de escolher 5 dos números 1, 2, 3, …, 52 sem repetição é:
a) entre 1 e 2 milhões.
b) entre 2 e 3 milhões.
c) entre 3 e 4 milhões.
d) menos de 1 milhão.
e) mais de 10 milhões.
14) (UDESC 2010) Doze equipes participarão de um torneio internacional de vôlei; os participantes foram divididos em dois grupos de seis equipes cada. A fase classificatória deste torneio prevê a realização de dois turnos. No primeiro turno, cada equipe jogará contra os adversários do seu próprio grupo e, no segundo, as equipes enfrentarão os times do outro grupo. Ao término da fase de classificação, os dois primeiros colocados de cada grupo avançarão para a fase final, que será disputada em turno único, num só grupo, com cada classificado jogando contra todos os outros times. O time que obtiver a primeira colocação na fase final será declarado campeão do torneio. De acordo com este regulamento, o total de jogos realizados durante o torneio é igual a:
a) 102
b) 66
c) 77
d) 72
e) 108
15) (Unirio) Recebi de uma editora um catálogo oferecendo em promoção a assinatura de 10 revistas. Gostaria de assinar todas, mas como não tenho posses para isso me contentarei com apenas 3. Quantas são as minhas opções?
a) 120 b) 144 c) 60 d) 240 e) 90
16) Três pessoas, A, B, C, chegam no mesmo dia a uma cidade onde há cinco hotéis H, H‚, H3, H4 e H5. Sabendo que cada hotel tem pelo menos três vagas, qual/quais das seguintes afirmações, referentes à distribuição das três pessoas nos cinco hotéis, é/são corretas?
(I) Existe um total de 120 combinações.
(II) Existe um total de 60 combinações se cada pessoa pernoitar num hotel diferente.
(III) Existe um total de 60 combinações se duas e apenas duas pessoas pernoitarem no mesmo hotel.
a) Todas as afirmações são verdadeiras.
b) Apenas a afirmação (I) é verdadeira.
c) Apenas a afirmação (II) é verdadeira.
d) Apenas as afirmações (I) e (III) são verdadeiras.
e) Apenas as afirmações (II) e (III) são verdadeiras.
b) 66
c) 77
d) 72
e) 108
15) (Unirio) Recebi de uma editora um catálogo oferecendo em promoção a assinatura de 10 revistas. Gostaria de assinar todas, mas como não tenho posses para isso me contentarei com apenas 3. Quantas são as minhas opções?
a) 120 b) 144 c) 60 d) 240 e) 90
16) Três pessoas, A, B, C, chegam no mesmo dia a uma cidade onde há cinco hotéis H, H‚, H3, H4 e H5. Sabendo que cada hotel tem pelo menos três vagas, qual/quais das seguintes afirmações, referentes à distribuição das três pessoas nos cinco hotéis, é/são corretas?
(I) Existe um total de 120 combinações.
(II) Existe um total de 60 combinações se cada pessoa pernoitar num hotel diferente.
(III) Existe um total de 60 combinações se duas e apenas duas pessoas pernoitarem no mesmo hotel.
a) Todas as afirmações são verdadeiras.
b) Apenas a afirmação (I) é verdadeira.
c) Apenas a afirmação (II) é verdadeira.
d) Apenas as afirmações (I) e (III) são verdadeiras.
e) Apenas as afirmações (II) e (III) são verdadeiras.









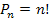
.jpg)
.png)
.png)
.png)
.png)
.png)


.gif)

