Cilindro - Área lateral e total e Volume
Cilindro Circular
Sejam α e β dois planos paralelos distintos, uma reta s secante a esses planos e um círculo C de centro O contido em α. Consideremos todos os segmentos de reta, paralelos a s, de modo que cada um deles tenha um extremo pertencente ao círculo C e o outro extremo pertencente a β.

Sejam α e β dois planos paralelos distintos, uma reta s secante a esses planos e um círculo C de centro O contido em α. Consideremos todos os segmentos de reta, paralelos a s, de modo que cada um deles tenha um extremo pertencente ao círculo C e o outro extremo pertencente a β.

A reunião de todos esses segmentos de reta é um sólido chamado de cilindro circular, limitado de bases C e C’ ou simplesmente cilindro circular.
Cilindro circular reto
No cilindro circular reto a geratriz forma com o plano da base um ângulo de 90º. No cilindro circular reto a medida h de uma geratriz é a altura do cilindro.
Cilindro circular reto
No cilindro circular reto a geratriz forma com o plano da base um ângulo de 90º. No cilindro circular reto a medida h de uma geratriz é a altura do cilindro.

O cilindro circular reto também é conhecido por cilindro de revolução, pois pode ser obtido pela revolução de 360º de uma região retangular em torno de um eixo.

Cilindro equilátero
O cilindro que possui as seções meridianas quadradas é chamado de cilindro equilátero.
No cilindro equilátero a altura é igual ao diâmetro da base: h = 2r.

O cilindro que possui as seções meridianas quadradas é chamado de cilindro equilátero.
No cilindro equilátero a altura é igual ao diâmetro da base: h = 2r.

Área Lateral e Área total de um cilindro circular reto
A superfície de um cilindro reto de altura h e raio da base r é equivalente à reunião de uma região retangular, de lados 2πr e h, com dois círculos de raio r. Observe a planificação do cilindro.

A superfície de um cilindro reto de altura h e raio da base r é equivalente à reunião de uma região retangular, de lados 2πr e h, com dois círculos de raio r. Observe a planificação do cilindro.

A área do retângulo equivalente à superfície lateral do cilindro é a área lateral Aℓ do cilindro, ou seja:
Aℓ = 2*π*r*h
A área total At do cilindro é igual à soma da área lateral Aℓ com as áreas das duas bases, ou seja:
At = 2*π*r*h + π*r2 + π*r2 → At = 2*π*r*h + 2π*r2
Volume do cilindro circular
O volume V de um cilindro circular de altura h e raio da base r é igual ao produto da área da base, πr2, pela altura h, isto é:
V = π*r2*h
Aℓ = 2*π*r*h
A área total At do cilindro é igual à soma da área lateral Aℓ com as áreas das duas bases, ou seja:
At = 2*π*r*h + π*r2 + π*r2 → At = 2*π*r*h + 2π*r2
Volume do cilindro circular
O volume V de um cilindro circular de altura h e raio da base r é igual ao produto da área da base, πr2, pela altura h, isto é:
V = π*r2*h
Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola
Graduado em Matemática
Equipe Brasil Escola
Questões resolvidas sobre Cilindros
1) Seja um cilindro circular reto de raio igual a 2 cm e altura 3 cm. Calcular a área lateral, área total e o seu volume.
Solução:
- Cálculo da Área lateral
Alat = 2 r h = 2
r h = 2  2.3 = 12
2.3 = 12  cm2
cm2 - Cálculo da Área total
Atot = Alat + 2 Abase
Atot = 12 + 2
+ 2  22 = 12
22 = 12  + 8
+ 8  = 20
= 20  cm2
cm2 - Cálculo do Volume
V = Abase × h = r2 × h
r2 × h
V = 22 × 3 =
22 × 3 =  × 4 × 3 = 12
× 4 × 3 = 12  cm33
cm33
2) (Cefet – SP) A figura indica o tambor cilíndrico de um aquecedor solar com capacidade de 1 570 litros.

Sabendo que 1 000 litros de água ocupam um volume de 1 m³ e adotado π = 3,14, determine a medida do raio r do cilindro.
Solução:
1570 litros → 1,57 m³
V = π * r² * h
1,57 = 3,14 * r² * 2
1,57 = 6,28 * r²
1,57 / 6,28 = r²
0,25 = r²
√r² = √0,25
r = 0,5 m
1,57 = 3,14 * r² * 2
1,57 = 6,28 * r²
1,57 / 6,28 = r²
0,25 = r²
√r² = √0,25
r = 0,5 m
A medida do raio do cilindro é de 0,5 metros ou 50 centímetros.
3) Uma indústria deseja fabricar um barril de óleo com formato cilíndrico cujo raio da base deve apresentar 40 cm de comprimento e sua altura será de 1,2 m. Para fabricação desse barril, a indústria utilizará chapas metálicas. Quantos metros quadrados de chapa serão necessários para fabricar um barril? (Use π = 3,14)
Solução:
A resolução desse problema consiste em determinar a área total desse barril, que apresenta o formato de um cilindro. Do enunciado do problema, obtemos:
h = 1,2 m
r = 40 cm = 0,4 m
St = ?
Pela fórmula da área total, temos que:
St = 2∙π∙r∙(h + r)
St = 2 ∙ 3,14 ∙ 0,4 ∙ (1,2 + 0,4)
St = 2 ∙ 3,14 ∙ 0,4 ∙ 1,6
St = 4,02 m2
Portanto, serão gastos, aproximadamente, 4,02 metros quadrados de chapa metálica para confeccionar um barril.
4) (USF-SP) Um cilindro circular reto, de volume 20π cm³, tem altura de 5cm. Sua área lateral, em centímetros quadrados, é igual a:
a)10π
b)12π
c)15π
d)18π
e)20π
Solução:
Na questão, podemos obter o raio do cilindro dessa forma:
Vcilindro = πR². h
Como a questão fornece o volume e a altura:
20π=πR².5
π dos dois lados podemos cortar, ficando:
20=5R²
R²=4
R=2
Tendo o raio, temos tudo, basta encontrar a área lateral:
Alateral = 2πRh
Alateral=2π2.5
Alateral=2π10
Alateral=20πcm³
5) Um reservatório em formato cilíndrico possui 6 metros de altura e raio da base igual a 2 metros. Determine o volume e a capacidade desse reservatório.

Solução:
V = π * r² * h
V = 3,14 * 2² * 6
V = 3,14 * 4 * 6
V = 75,36 m³
Temos que 1m³ corresponde a 1 000 litros, então 75,36 m³ é equivalente a 75 360 litros.
Volume do cilindro = 75,36 m³ (metros cúbicos)
Capacidade do cilindro = 75 360 litros
6) (Vunesp – SP) Um tanque subterrâneo, que tem o formato de um cilindro circular reto na posição vertical, está completamente cheio com 30 m³ de água e 42 m³ de petróleo. Considerando que a altura do tanque é de 12 metros, calcule a altura da camada de petróleo.
V = 3,14 * 2² * 6
V = 3,14 * 4 * 6
V = 75,36 m³
Temos que 1m³ corresponde a 1 000 litros, então 75,36 m³ é equivalente a 75 360 litros.
Volume do cilindro = 75,36 m³ (metros cúbicos)
Capacidade do cilindro = 75 360 litros
6) (Vunesp – SP) Um tanque subterrâneo, que tem o formato de um cilindro circular reto na posição vertical, está completamente cheio com 30 m³ de água e 42 m³ de petróleo. Considerando que a altura do tanque é de 12 metros, calcule a altura da camada de petróleo.

Solução:

Calculando a altura da camada de petróleo

A camada de petróleo tem uma altura de 7 metros.
7) (questão Enem-2011) É possível usar água ou comida para atrair as aves e observá-las. Muitas pessoas costumam usar água com açúcar, por exemplo, para atrair beija-flores, Mas é importante saber que, na hora de fazer a mistura, você deve sempre usar uma parte de açúcar para cinco partes de água. Além disso, em dias quentes, precisa trocar a água de duas a três vezes, pois com o calor ela pode fermentar e, se for ingerida pela ave, pode deixá-la doente. O excesso de açúcar, ao cristalizar, também pode manter o bico da ave fechado, impedindo-a de se alimentar. Isso pode até matá-la.
ciência Hoje das crianças. FNDE; Instituto Ciência Hoje, ano 19, n. 166, mar. 1996.
Pretende-se encher completamente um copo com a mistura para atrair beija-flores. O copo tem formato cilíndrico, e suas medidas são 10 cm de altura e 4 cm de diâmetro, A quantidade de água que deve ser utilizada na mistura é cerca de (utilize π(pi) = 3)
a) 20 mL. b) 24 mL. c) 100 mL. d) 120 mL. e) 600 mL.
SOLUÇÃO:
Precisamos calcular o volume do Cilindro de altura 10cm e diâmetro 4cm. Lembre que o raio é metade do diâmetro, portanto seu raio R = 2cm.

Como o enunciado diz, será necessário usar uma parte de açúcar para cinco partes de água.
1 parte de açucar + 5 partes de água = 120cm3
6 partes = 120 cm3
Cada parte corresponderá a 120/6 = 20cm3
Como teremos cincos partes de água então a quantidade de água que deve ser utilizada na mistura será cerca de 5 x 20 = 100cm3.
Gabarito Letra C.
8) Determine o volume de um cilindro circular reto cujo raio da base mede 5 m e altura 3 m.
Solução:
V = π * (5 m)² * 3 m = 75 π m³
9) (FGV) Em certa loja, as panelas são anunciadas de acordo com sua capacidade. Uma panela dessa loja, com a etiqueta "4 litros", tem 20cm de diâmetro. A altura dessa panela é aproximadamente:
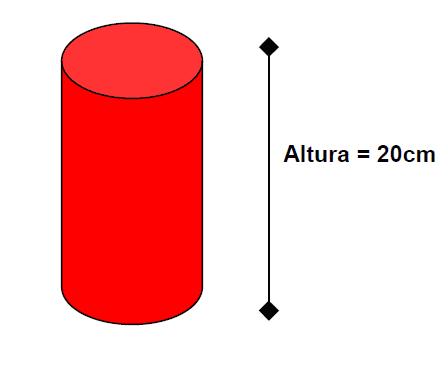 altura é de 20cm.
altura é de 20cm.
Solução:
A(base) = pi.r² = pi.2² = 4 pi cm²
A(lateral) = 2.pi.r.h = 2.pi.2.3 = 12 pi cm²
A(total) = A(lateral) + 2 A(base) = 12pi + 8pi = 20 pi cm²
Volume = A(base).h = pi.r²h = pi.4.3 = 12 pi cm³
a) 7cm b) 9cm c) 11cm d) 13cm e) 15cm.
Solução:
O volume 4 litros corresponde em 4dm3 ou 4000cm3. O raio da panela mede 10cm. Aplicando a fórmula do volume do cilindro, temos:
(V cilindro = π R² . h 4000 40 ~
(V cilindro = 400 --- > ( 3,14 ) . (10) ² . h = 4000 -- > h = -------------- = ----- = 12,73 cm
( 3,14) . (100) 3,14
10) Achar a área total da superfície de um cilindro reto, sabendo que o raio da base é de 10cm e a
 altura é de 20cm.
altura é de 20cm.Solução:
A área de cada base é dada por Ab = πx r² ≈ 3,14 x 100 = 314cm² .
Quando planificamos a superfície lateral de um cilindro, obtemos um retângulo no qual os lados têm a mesma altura h do cilindro e o comprimento 2π da circunferência de uma das bases. Assim, temos C = 2 x π x 10 ≈ 62,8cm. Desse modo, a área da superfície
lateral é Al ≈ 62,8 x 20 = 1.256cm².Assim, a área total da superfície
desse cilindro é At ≈ 314 + 314 + 1.256, o que resulta em
At ≈ 1.884cm²
Quando planificamos a superfície lateral de um cilindro, obtemos um retângulo no qual os lados têm a mesma altura h do cilindro e o comprimento 2π da circunferência de uma das bases. Assim, temos C = 2 x π x 10 ≈ 62,8cm. Desse modo, a área da superfície
lateral é Al ≈ 62,8 x 20 = 1.256cm².Assim, a área total da superfície
desse cilindro é At ≈ 314 + 314 + 1.256, o que resulta em
At ≈ 1.884cm²
11) (FATEC) Sabe-se que um cilindro de revolução de raio igual a 10 cm, quando cortado por um plano paralelo ao eixo, a uma distância de 6 cm desse eixo, apresenta uma secção retangular equivalente à base. O volume desse cilindro, em centímetros cúbicos, é:
a) 1250π b)1250π² c)6,25π² d) 625π e)625π²
Solução:
A figura mostra a secção (azul) a 6cm do eixo. Ela é um retângulo de dimensões (2x) e h. O valor de “x” pode ser calculado pela relação de Pitágoras:
10² = 6² + x² ---- > x = √100 - 36 = √64 = 8 cm
Logo (2x) = 16cm
Como a secção é equivalente à base, suas áreas são iguais:
{Abase =πR² = π (10)² =100 π
{Asecção = (2x) . h = 16. h
( 100 π ) 10000 π ²
V= π R² . h = π (10)² .-------- =-------------- = 625 π² cm ³
( 16 ) 16
12) Seja um cilindro circular reto de raio igual a 2cm e altura 3cm. Calcular a área lateral, área total e o seu volume.
Solução:
A(base) = pi.r² = pi.2² = 4 pi cm²
A(lateral) = 2.pi.r.h = 2.pi.2.3 = 12 pi cm²
A(total) = A(lateral) + 2 A(base) = 12pi + 8pi = 20 pi cm²
Volume = A(base).h = pi.r²h = pi.4.3 = 12 pi cm³
13) Um caldeirão cilíndrico tem 40 cm de diâmetro e 15 cm de altura e está lotado em sua capacidade máxima de doce. Cláudia vai encher potinhos cônicos com esse doce. Se cada potinho tem 6 cm de altura e 4 cm de diâmetro da base, quantos potinhos serão necessários para colocar todo esse doce?
Solução:
Neste quesito é necessário que saibamos calcular o volume tanto de um cone, quanto de um cilindro, pois a razão destes volumes é a resposta deste problema.
Para calcularmos o volume do cilindro que contém o doce vamos utilizar a seguinte fórmula:
O volume dos potinhos que irão conter os doces será calculado através da fórmula:
Note que o volume do cone equivale a 1/3 do volume do cilindro.
Como o diâmetro do caldeirão é de 40 cm, seu raio que é a metade disto mede 20 cm. A altura sabemos que é de15 cm, portanto o seu volume é igual a:
Não realizamos a multiplicação por 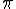 , pois poderemos simplificá-lo com o
, pois poderemos simplificá-lo com o 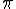 que existe no cálculo do volume do cone.
que existe no cálculo do volume do cone.
Para o cálculo do volume do potinho temos um raio de 2 cm, que é a metade dos 4 cm do diâmetro e uma altura de 6 cm:
Dividindo um volume pelo outro vamos obter a quantidade necessária de potinhos:
Portanto:
Serão necessários 750 potinhos para colocar todo esse doce.
14) Considere um cilindro circular reto de 8 cm de altura e raio da base medindo 5 cm. Determine a capacidade desse cilindro. (Utilize π = 3,14)
Solução:
De acordo com o enunciado do problema, temos que:
h = 8 cm
r = 5 cm
Calcular a capacidade é o mesmo que determinar o volume do cilindro.
Utilizando a fórmula do volume, obtemos:
V = π ∙ r² ∙ h
V = 3,14 ∙ 52∙8
V = 3,14 ∙ 25 ∙ 8
V = 628 cm³.
15) Uma indústria de embalagens deseja fabricar uma lata de tinta cilíndrica com raio da base medindo 5 cm de comprimento e com capacidade para 1 litro. Qual deverá ser o comprimento da altura dessa embalagem? (Use π = 3,1)

Solução:
De acordo com o problema, o volume desse cilindro deverá ser de 1 litro ou 1 dm3. Sabemos que o raio da base será de 5 cm, que equivale a 0,5 dm. Utilizando a fórmula do volume, teremos:
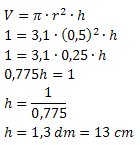
Portanto, a lata deverá ter uma altura de, aproximadamente, 13 cm.








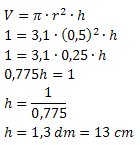
Portanto, a lata deverá ter uma altura de, aproximadamente, 13 cm.
16) (Petrobrás) Um cilindro circular reto possui altura igual ao raio de sua base. Se a razão entre o volume do cilindro, dado em metros cúbicos, e a sua área total, dada em metros quadrados, é igual a 2 metros, então a área lateral do cilindro, em m2, é igual a
(A) 128π
(B) 64π
(C) 48π
(D) 32π
(E) 16π
Solução:
Para resolvermos este problema, poderíamos fazer um desenho da situação, mas não é necessário! Veja:
Sejam h e r a altura e raio da base do cilindro, respectivamente.
Do problema, temos que h = r.
Temos ainda que a razão entre o volume V e a área total A do cilindro é 2, daí podemos escrever
O problema pede a área lateral do cilindro Al , sabemos que a área lateral do cilindro é dada por
Mas, h = r, então vamos substituir.
Veja que na última expressão acima para encontrarmos a medida da área lateral, dependemos da medida do raio r. Então, vamos determinar a medida do raio r. Mas, antes lembre-se:
Como h = r, temos:
Bem, r é a medida do raio, então deve ser maior do que zero, portanto r = 8m.
Agora, substituindo para determinarmos a área lateral:
Muito bom !
ResponderExcluirObrigado! Agora vou fazer meu trabalho
ResponderExcluirmuito bom os exercícios me ajudou muito
ResponderExcluirExcelente, valeu mesmo.
ResponderExcluirBom demais, acertei a maioria e estou muito feliz! Muito bom mesmo!
ResponderExcluir