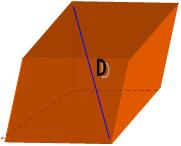
Cubo é todo paralelepípedo com superfície quadrada.
O cubo tem os seguintes elementos:
* 6 faces, que são quadrados geometricamente iguais;
* 12 arestas iguais, que são segmentos de reta;
* 8 vértices, que são pontos.
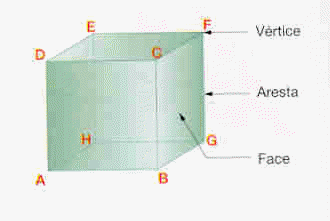
Para construir um cubo basta conhecer a medida de uma aresta.
Chama-se diagonal do cubo, D, ao segmento de reta que une dois vértices não pertencentes à mesma face.

A diagonal D do cubo é a hipotenusa do triângulo retângulo de catetos a e d: D2 = d2 + a2. Mas d é a hipotenusa do triângulo retângulo de catetos iguais a a, sendo a a medida da aresta do cubo, logo, d2 = a2 + a2, ou seja, d2 = 2a2. Então, D2 = 2a2 + a2 = 3a2, donde temos que o comprimento da diagonal do cubo é dada por D =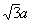 .
.
A área da superfície do cubo pode calcular-se facilmente atendendo ao fato das suas faces serem 6 quadrados iguais.

Sendo a o comprimento da aresta do cubo, a área de cada face será a2, e portanto, temos:
* Área lateral do cubo:
A área lateral do cubo é a soma das áreas das faces laterais, sendo dada por:
Al = 4a2 , onde: Al - área lateral
* Área total do cubo:
A área total do cubo é a soma da área lateral com a área das duas bases, ou seja:
At = Al + 2Ab= 4a2 + 2a2 = 6a2, onde: At - área total
Al = 4a2 - área lateral
Ab = a2 - área da base
* 6 faces, que são quadrados geometricamente iguais;
* 12 arestas iguais, que são segmentos de reta;
* 8 vértices, que são pontos.

Para construir um cubo basta conhecer a medida de uma aresta.
Chama-se diagonal do cubo, D, ao segmento de reta que une dois vértices não pertencentes à mesma face.

A diagonal D do cubo é a hipotenusa do triângulo retângulo de catetos a e d: D2 = d2 + a2. Mas d é a hipotenusa do triângulo retângulo de catetos iguais a a, sendo a a medida da aresta do cubo, logo, d2 = a2 + a2, ou seja, d2 = 2a2. Então, D2 = 2a2 + a2 = 3a2, donde temos que o comprimento da diagonal do cubo é dada por D =
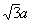 .
.A área da superfície do cubo pode calcular-se facilmente atendendo ao fato das suas faces serem 6 quadrados iguais.

Sendo a o comprimento da aresta do cubo, a área de cada face será a2, e portanto, temos:
* Área lateral do cubo:
A área lateral do cubo é a soma das áreas das faces laterais, sendo dada por:
Al = 4a2 , onde: Al - área lateral
* Área total do cubo:
A área total do cubo é a soma da área lateral com a área das duas bases, ou seja:
At = Al + 2Ab= 4a2 + 2a2 = 6a2, onde: At - área total
Al = 4a2 - área lateral
Ab = a2 - área da base
Saiba Mais no GrupoEscolar.com: http://www.grupoescolar.com/pesquisa/cubo.html
CUBO - VOLUME
O cubo é denominado hexaedro regular e é um dos cinco sólidos de Platão. Por ser considerado um sólido, possui volume.
Dizemos que volume é a quantidade de espaço ocupado por um corpo ou a capacidade de armazenamento que um corpo possui. O volume de um cubo depende da medida de sua aresta, consideramos apenas uma medida, pois o cubo possui todas as arestas de tamanhos iguais e seu volume é apresentado pela expressão V = a³, onde a corresponde à medida da aresta.
O volume de um cubo é determinado através do produto da área da base pela altura, como já foi dito que as arestas do cubo possuem medidas iguais, então temos que V = Ab * aou V = a * a * a → V = a³. Observe:
Dizemos que volume é a quantidade de espaço ocupado por um corpo ou a capacidade de armazenamento que um corpo possui. O volume de um cubo depende da medida de sua aresta, consideramos apenas uma medida, pois o cubo possui todas as arestas de tamanhos iguais e seu volume é apresentado pela expressão V = a³, onde a corresponde à medida da aresta.
O volume de um cubo é determinado através do produto da área da base pela altura, como já foi dito que as arestas do cubo possuem medidas iguais, então temos que V = Ab * aou V = a * a * a → V = a³. Observe:
.jpg)
As unidades mais usadas para expressar capacidade são as seguintes: m³ (metro cúbico), cm³ (centímetro cúbico), dm³ (decímetro cúbico). Onde respeitam as seguintes relações:
1 m³ = 1000 litros
1 dm³ = 1 litro
1 cm³ = 1 mililitro ou 1 ml
De acordo com as seguintes relações, concluímos que:
Um cubo formado por arestas medindo 1 metro (m) cada, possui capacidade de 1000 litros, pois: V = 1m * 1m * 1m = 1m³.
Um cubo formado por arestas medindo 1 decímetro (dm) cada, possui capacidade de 1 litro, pois: V = 1dm * 1dm * 1dm = 1dm³ = 1 litro.
Um cubo formado por arestas medindo 1 centímetro (cm) cada, possui capacidade de 1 ml, pois: V = 1cm * 1cm * 1cm = 1cm³ = 1 ml.
Exemplo
Dado um cubo de 10 cm de aresta, determine quantas bolinhas de diâmetro igual a 1cm ele comporta.
Resolução:
De acordo com o que foi demonstrado, temos que o volume total do cubo corresponde a:
V = 10cm * 10cm * 10cm = 1000 cm³. Como a bolinha possui diâmetro medindo 1cm, podemos formar as arestas do cubo com 10 bolinhas enfileiradas. Observe:
1 m³ = 1000 litros
1 dm³ = 1 litro
1 cm³ = 1 mililitro ou 1 ml
De acordo com as seguintes relações, concluímos que:
Um cubo formado por arestas medindo 1 metro (m) cada, possui capacidade de 1000 litros, pois: V = 1m * 1m * 1m = 1m³.
Um cubo formado por arestas medindo 1 decímetro (dm) cada, possui capacidade de 1 litro, pois: V = 1dm * 1dm * 1dm = 1dm³ = 1 litro.
Um cubo formado por arestas medindo 1 centímetro (cm) cada, possui capacidade de 1 ml, pois: V = 1cm * 1cm * 1cm = 1cm³ = 1 ml.
Exemplo
Dado um cubo de 10 cm de aresta, determine quantas bolinhas de diâmetro igual a 1cm ele comporta.
Resolução:
De acordo com o que foi demonstrado, temos que o volume total do cubo corresponde a:
V = 10cm * 10cm * 10cm = 1000 cm³. Como a bolinha possui diâmetro medindo 1cm, podemos formar as arestas do cubo com 10 bolinhas enfileiradas. Observe:
.jpg)
Portanto, o cubo com 10 cm de aresta comporta 1000 bolinhas com 1 cm de diâmetro.
Por Marcos Noé Pedro Da Silva
EM Http://Www.Mundoeducacao.Com.Br/Matematica/Volume-Cubo.Htm
Questões resolvidas sobre cubo
1) (UFOP–MG) A área total de um cubo cuja diagonal mede 5√3 cm é:
a) 140 cm²
b) 150 cm²
c) 120√2 cm²
d) 100√3 cm²
e) 450 cm²
b) 150 cm²
c) 120√2 cm²
d) 100√3 cm²
e) 450 cm²
Solução:
A diagonal de um cubo pode ser calculada através da seguinte expressão matemática:
d = a√3. Foi fornecido que a medida da diagonal do cubo é 5√3, então:
d = a√3. Foi fornecido que a medida da diagonal do cubo é 5√3, então:

A medida da aresta desse cubo mede 5 cm. Dessa forma, cada face do cubo medirá:
A = 5 * 5
A = 25 cm²
A = 25 cm²
Sabendo que o cubo possui 6 faces laterais temos:
Área Total: 6 * 25
Área Total: 150 cm²
Área Total: 150 cm²
A área total do cubo com diagonal medindo 5√3 cm é igual a 150 cm².
Resposta correta: item b.
2) A área total de um cubo é 54 cm². Calcule a medida da diagonal desse cubo.
Solução:
Ac = 6a² dc = a√3
54 = 6a² dc = 3√3cm²
54 /6 = a²
a = √9
a =3 cm
3) Se a soma das medidas de todas as arestas de um cubo é 60 cm,então o volume desse cubo, em centímentros cúbicos, é:
a) 125 cm³
b) 100 cm³
c) 75 cm³
d) 60 cm³
e) 25 cm³
Solução:
12 arestas
60 cm / 12 = 5
V = 5³ = 125 cm³
Letra a) 125 cm³
a) 125 cm³
b) 100 cm³
c) 75 cm³
d) 60 cm³
e) 25 cm³
Solução:
12 arestas
60 cm / 12 = 5
V = 5³ = 125 cm³
Letra a) 125 cm³
4) (Fuvest-SP) Dois blocos de alumínio, em forma de cubo, com arestas medindo 10 cm e 6 cm, são levados juntos à fusão e em seguida o alumínio líquido é moldado como um paralelepípedo reto de arestas 8 cm, 8 cm e x cm. O valor de x é:
a) 16 m d) 19 m
b) 17 m e) 20 m
c) 18 m
Solução:
Resposta: D
Pelo enunciado, o volume do paralelepípedo é igual à soma dos volumes dos cubos.
Assim,
8 • 8 • x = 63 + 103
64 x = 216 + 1 000
64 x = 1 216 x = 19
5) (Unirio-RJ) Uma caixa d´água tem forma cúbica com 1 metro de aresta. De quanto baixa o nível da água ao retirarmos 1 litro de água da caixa?
Solução:
6) A terceira parte do volume de um cubo é de 9 metros cúbicos. Logo a medida de sua aresta será:
A) 3 m
B) 6 m
C) 9 m
D) 18 m
E) 27 m
Solução:
1/3 * V = 9 m³
V = 3 * 9 = 27 m³
V = a³ = 27 m³ a
V = 3 m
7) Observe o dado ilustrado abaixo, formado a partir de um cubo, e com suas seis faces numeradas de 1 a 6.

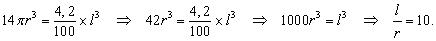
9) Uma caixa d’água possui as seguintes dimensões:Altura = 28 cm; Comprimento = 0,8 m; Largura : 20 cm
Qual o volume da caixa d’água em metros cúbicos?
a) 16 m d) 19 m
b) 17 m e) 20 m
c) 18 m
Solução:
Resposta: D
Pelo enunciado, o volume do paralelepípedo é igual à soma dos volumes dos cubos.
Assim,
8 • 8 • x = 63 + 103
64 x = 216 + 1 000
64 x = 1 216 x = 19
5) (Unirio-RJ) Uma caixa d´água tem forma cúbica com 1 metro de aresta. De quanto baixa o nível da água ao retirarmos 1 litro de água da caixa?
Solução:
V = a³
V = 1³
V = 1 m³
1 m³ equivale a 1000 litros. Então ao retirarmos 1 litro vamos ter 999 litros.
transformando para m³ obtemos a resposta da questão 0,999 m³.6) A terceira parte do volume de um cubo é de 9 metros cúbicos. Logo a medida de sua aresta será:
A) 3 m
B) 6 m
C) 9 m
D) 18 m
E) 27 m
Solução:
1/3 * V = 9 m³
V = 3 * 9 = 27 m³
V = a³ = 27 m³ a
V = 3 m
7) Observe o dado ilustrado abaixo, formado a partir de um cubo, e com suas seis faces numeradas de 1 a 6.

Esses números são representados por buracos deixados por semi-esferas idênticas retiradas de cada uma das faces. Todo o material retirado equivale a 4,2% do volume total do cubo.
Considerando p = 3, a razão entre a medida da aresta do cubo e a do raio de uma das semi-esferas, expressas na mesma unidade, é igual a:
(A) 6
(B) 8
(C) 9
(D) 10
Solução:
Considere-se 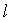 a medida da aresta do cubo e r a do raio de cada semi-esfera. O volume do cubo é
a medida da aresta do cubo e r a do raio de cada semi-esfera. O volume do cubo é 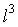 e o de cada semi-esfera
e o de cada semi-esfera 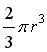 .
.
O número de semi-esferas retiradas desse cubo é igual a 1 + 2 + 3 + 4 + 5 + 6 = 21, e o volume de todas elas é igual a 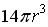 . Como esse volume equivale a 4,2 % do volume total do cubo,
. Como esse volume equivale a 4,2 % do volume total do cubo,
Percentual de acertos: 16,98%
8) Calcule o volume de um cubo, em m3 e ml, sabendo que ele possui arestas 0,8 m.
Solução:
V = c . L . h
V = 0,8 . 0,8 . 0,8
V = 0,512 m3
1 m3 ............1000L
0,512 m3...........X
X = 0,512 . 1000
X = 512 Litros
1L .............1000ml
512 L............X
X = 1000 . 512
X = 512000 ml
Qual o volume da caixa d’água em metros cúbicos?
Solução:
V = c . L .h
V = 0,8 m . 0,2 m . 0,28 m
V = 0,0448 m3
10) O Cubo, também chamado de hexaedro, é um poliedro regular com 6 faces. Um determinado cubo tem volume de 343 unidades de volume. A área desse cubo tem quantas unidades de área?
a) 5.716 b) 210 c) 196 d) 294 e) 147
Solução:




depois dessa vou fumar um green e ficar de boa
ResponderExcluirmuito bom , perguntas com as soluções ! só agradec tio
ResponderExcluirBom
ResponderExcluirGostei bastante
ResponderExcluir