Questões resolvidas de vestibulares sobre Trapézio

Artigo sobre o Trapézio, área, classificação e  Mediana de Euler.

Chamamos de trapézio o quadrilátero que possui bases paralelas.

O trapézio pode ser classificado como isósceles, também chamado de simétrico, escaleno, ou retângulo.

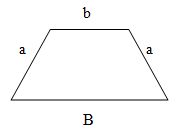
Trapézio Isósceles ou simétrico

É o trapézio que possui os lados não paralelos iguais:

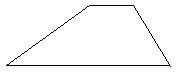
Trapézio Escaleno

É o trapézio que possui todos os lados desiguais.

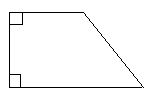
Trapézio Retângulo

É o trapézio que possui dois ângulos retos (90º)

Base média do trapézio

Chamamos de base média do trapézio ao segmento paralelo às bases, que une os pontos médios dos lados não paralelos do trapézio.

O valor da base média é igual à semi-soma das bases do trapézio, isto é, , onde “B” é a medida do comprimento da base maior e “b” é a medida  do comprimento da base menor do trapézio.

Mediana de Euler (M_e)

Chama-se mediana de Euler (M_e) ao segmento que une os meios das diagonais do trapézio e seu valor pode ser obtido pela semi-diferença das bases do trapézio, isto é, .

Média harmônica das bases (M_h)

A média harmônica das bases é o segmento que passa pelo ponto de encontro das diagonais do trapézio, paralelo às bases e compreendido entre os lados oblíquos. A medida da Média Harmônica pode ser obtida por .

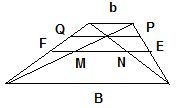
Na figura a seguir, pode-se observar a Base Média, a Mediana de Euler e a Média Harmônica das bases.

Mediana de Euler: MN
Base Média: EF
Média Harmônica das Bases: PQ

Área de um Trapézio

Considere um trapézio de base maior B, base menor b e altura h.

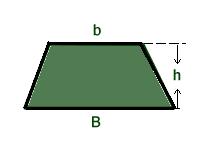
A área do trapézio será dada por:

Observe que a área do trapézio é a metade do produto entre a soma das bases pela altura.

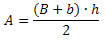
Exemplo: Calcule a área de um trapézio de bases medindo 10 cm e 5 cm e altura 6 cm.

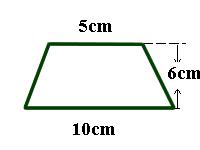
Solução: O problema nos forneceu

B = 10 cm
b = 5 cm
h = 6 cm

Substituindo esses valores na fórmula da área, obtemos:

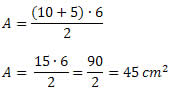
Questões de vestibulares resolvidas sobre trapézio

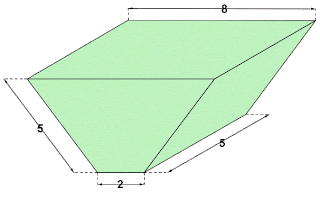
1) (PUC-SP) Um tanque de uso industrial tem a forma de um prisma cuja base é um trapézio isósceles. Na figura a seguir, são dadas as dimensões do prisma em metros:

O volume desse tanque em metros cúbicos é:

a)      50 b)      60

c)      80 d)      100

e)      120

a = cateto do triângulo retângulo formado com a altura do trapézio isósceles.

a=(8-2)/2⇒a=3 
h = altura do triângulo.
h²+3²=5²⇒h²=16⇒h=4 
A_b = área da base do prisma (tanque)

A_b=(8+2)4/2⇒A_b=20 
V = volume do prisma

V=20*5⇒V=100 

Resposta = d)

2)  Determine a medida da base maior de um trapézio com 150 cm² de área, 10 cm de altura e base menor medindo 12 cm.

Dados do problema:

A = 150 cm²     h = 10 cm       b = 12 cm        B = x

Solução:

150 = (B + 12) . 10/2

300 = (B + 12) . 10

300/10 = B + 12

B + 12 = 30

B = 30 – 12

B = 18 cm

Temos, B = 18 cm

3) Calcular a área do trapézio isósceles traçado ao lado se todos os seus lados são tangentes à circunferência e as medidas são dadas em cm.

Solução:

Vamos construir um triângulo isósceles com o prolongamento dos lados não paralelos do trapézio, de acordo com a figura abaixo. 
Tomaremos h=AE e r o raio da circunferência inscrita no trapézio.
BC=18 e DF=8, logo GC=9 e EF=4.
Como o trapézio BCFD é isósceles, o triângulo ABC é isósceles.
O triângulo AGC é retângulo com ângulo reto em G.
O triângulo AEF é retângulo com ângulo reto em E e por semelhança de triângulos, temos que:

AE / EF = AG / GC implica que h / 4 = (h + 2r) / 9
h = 8r / 5

O triângulo ATO tem um ângulo reto em T, porque T é ponto de tangência. Este triângulo ATO também é semelhante ao triângulo AGC, logo:AT/TO = AG/GC
m(AT)/r = (h+2r)/9 (*)

Acontece que AT = R[h²+2hr] = R[16r²/25 + 2r(8r)/5] = 12r / 5

Substituindo este valor em (*), obtemos:

12r / 5r = (h+2r) / 9
12/5 = (8r/5 + 2r) / 9
r = 6

A_trapézio = (B_maior + B_menor).h/2
A_trapézio = (18+8).2.6/2 = 78

4) Um trapézio isósceles com bases medindo 12 cm e 16 cm está inscrito em uma circunferência de raio 10 cm. Calcular a área do trapézio, se o centro da circunferência não está no interior do trapézio. 

Solução:



Na figura acima a altura h do trapézio é dada por h=b-a, onde: 

a² = 10² - 8² = 36
a = 6
b² = 10² - 6² = 64
b=8
h = 8 - 6 = 2 cm

A = (1/2)(B+b)h = (1/2)(16+12).2 = 28 cm².

5) (UFPE) A área do trapézio (figura abaixo) é igual a

 

A) 86
B) 96
C) 106
D) 116
E) 126

Resposta

6) A figura mostra um retângulo ABEF, com BC = 10, CF = 5, e CD = 4. Qual a medida do perímetro do trapézio ABCD?

A) 16
B) 22
C) 28
D) 32
E) 36



Resposta: A primeira é que, como o quadrilátero ABCD é um trapézio, medida CD é paralelo a base AB do retângulo.

Logo o triangulo DCF é retangulo com vértice D.

Usaremos o teorema de Thales 2 vezes, vejamos:


No triângulo retângulo DCF , verificamos Trio Pitagórico 3-4-5







Por Thales: 5/4 = 15/y
resulta Y=12

Por Thales: 3/4 = (3+x)/12 resulta X=6

Périmetro do Trapézio = X+Y+10+4=6+12+10+4 = 32

Alternativa D)

7) Seja ABCD um trapézio retângulo. Sabendo-se que a base menor mede três centímetros, a base maior mede quinze centímetros e que a altura relativa à base maior mede cinco centímetros, podemos afirmar corretamente que o comprimento do lado do trapézio que não é perpendicular às bases mede quantos centímetros?

Solução:

 Para resolver esta questão precisamos saber o que é um trapézio retângulo e também conhecer o teorema de Pitágoras.

A partir dos dados do enunciado podemos desenhar o trapézio retângulo ao lado:

Repare que identificamos o lado desconhecido utilizando a letra x.

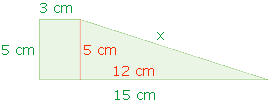
Se traçarmos uma linha vertical paralela ao lado de 5 cm conforme mostrado na figura, iremos dividir o trapézio retângulo em um retângulo e um triângulo retângulo:

Então para conhecermos o comprimento do lado x, basta utilizarmos o teorema de Pitágoras para calcularmos o comprimento da hipotenusa do triângulo retângulo resultante da separação dotrapézio retângulo em duas partes.

O teorema de Pitágoras é representado pela equação:

Relacionando as variáveis temos:

Substituindo-as e resolvendo a equação:

Portanto:

O comprimento do lado do trapézio que não é perpendicular às bases mede 13 cm centímetros.

8) Determine a medida da base maior de um trapézio com 150 cm² de área, 10 cm de altura e base menor medindo 12 cm.

Solução:
Dados
A = 150 cm²
h = 10 cm
b = 12 cm
B = ?

Substituindo os dados na fórmula da área, obtemos:

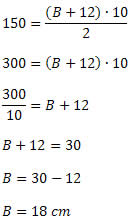
Exemplo 3. Num trapézio de 8 cm de altura, a base maior é o dobro da base menor. Determine a medida dessas bases sabendo que a área desse trapézio é 180 cm².

Solução:

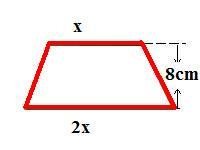
Dados

A = 180 cm²
h = 8 cm
b = x
B = 2x

Substituindo os dados na fórmula da área do trapézio, obtemos:

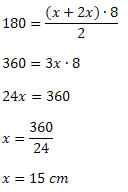
Assim, b = 15 cm e B = 30 cm.

Fonte: www.infoescola.com/

           ensinodematemtica.blogspot.com.br