Radiciação - propriedades e operações (com exercícios)

Radiciação

A radiciação é a operação inversa da potenciação. É muito utilizada na obtenção de solução de equações e na simplificação de expressões aritméticas e algébricas. Vamos definir essa operação e analisar suas propriedades.
Dados um número real não negativo x e um número natural n ≥ 1, chama-se raiz enésima de x o número real não negativo y tal que yⁿ = x. O símbolo utilizado para representar a raiz enésima de x é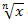  e é chamado de radical. Nesse símbolo, x é o radicando e n é o índice.

Pela definição de radiciação, temos que:

Exemplo 1:

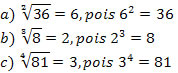
Propriedades da radiciação

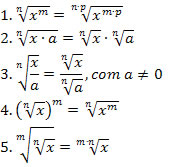
Exemplo 2. Simplifique a expressão

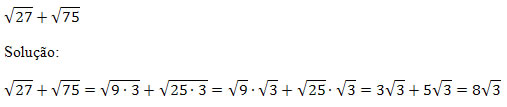
Exemplo 3. Verifique as propriedades da radiciação.

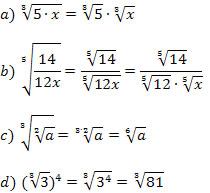
Exemplo 4. Obtenha a forma mais reduzida possível da expressão:

Solução: Podemos reescrever cada uma das raízes utilizando as propriedades da radiciação.

Racionalização de denominadores

Em alguns cálculos, você pode se deparar com raízes no denominador da fração. Para que você possa prosseguir com os cálculos, é conveniente que você elimine essas raízes do denominador - processo chamado de racionalização de denominadores. Isto é, transforma-se um denominador irracional em racional.

 o denominador  é um número irracional e deve ser eliminado.

Atenção: o importante é eliminar a raiz (que pode ser quadrada, cúbica, etc), mantendo uma fração "equivalente", ou seja, que representa o mesmo valor.

Uma dica é multiplicar tanto o numerador (parte de cima), quanto o denominador pelo mesmo número, o que não interfere na igualdade. Se a fração anterior for multiplicada em cima e em baixo por  ficará:

. Note que  é igual a 1, logo a multiplicação de um número por 1 não o altera.

Prosseguindo:

Como se pode notar o denominador agora é um número racional (3).

Raízes não-quadradas

Para eliminar raízes cúbicas, ou de outros índices diferentes de 2 (lembre-se: raiz quadrada é, na verdade, uma raiz de índice 2!), é necessário utilizar um artifício.

Multiplique, no numerador e no denominador, por uma raiz de mesmo radicando (o número dentro da raiz) e cujo índice seja equivalente ao índice da raiz original menos um. Por exemplo:

Soma de raízes no denominador

Veja:

Deve-se multiplicar por .

Isso porque a multiplicação de  por  é, na verdade, a multiplicação de (a + b). (a - b), um produto notável, cujo resultado é (a² - b²) - isto é, os radicais somem!

Exemplo 1. Racionalize as seguintes frações:

Racionalizar a fração é fazer com que no denominador não exista uma raiz enésima de um número. 

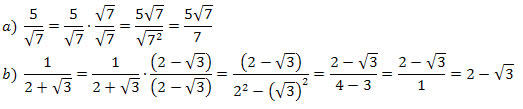
Exemplo 2. Racionalize as frações:

Operações com radicais

Radicais como potências de expoente fraccionário         

             

São da forma ⁿ√a^m =a ^m/n , com a>0, n ∈ ℕe m/n ∈ℚ  

                

Exemplos:

                        ⁵√2^-3 = 2^-3/5

                        3⁵ =3 ^15/3 = ³ √(3 ¹⁵)       

                       2 ^–1/4 = (1/2)^1/4 = ⁴√(1/2) ou 2^-1/4 =⁴√2^-1

Multiplicação de  radicais

         

Aqui, os radicais têm que ter o mesmo índice, sendo da forma  

ⁿ√a´ⁿ√b = ⁿ√(ab)

  com a, b ∈ ℝ⁺ e n∈ℕ.

            Exemplos:

                     √2´√3´√5 = √(2´3)´√5 = √6´√5 = √(6´5) = √30

                     √2´⁴√3 = ^2´2√2² ´⁴√3 = ⁴√4´ ⁴√3 = ⁴√12

          

Divisão de radicais    

           

Tal como na multiplicação, também os radicais aqui  têm de ter o mesmo índice. Assim, são da forma

  ⁿ√a ¸ⁿ√b = ⁿ√ (a/b)

  com a, b ∈ℝ⁺ e n∈ℕ.

           

 Exemplo:

                    ³√6 ¸ ³√3´³√2 = ³√ (6/3)´³√2 = ³√2´³√2 = ³√4

         

Adição de expressões com radicais     

            

Só é possível simplificar a soma de expressões com radicais se estes tiverem o mesmo índice e o mesmo radicando. As operações de simplificação de radicais são: divisão do índice do radical e o expoente do radicando pelo seu máximo divisor comum ou passagem para fora do radical todos os factores possíveis.

 Exemplos:

                    √2-√5+3√2+7√5 = √2+3√2-√5+7√5 = (1+3) √2+(-1+7)√5 = 4√2+6√5

                    ³√5+2⁹√5³ = ³√5 + 2³√5  = (1+2) ³√5  = 3 ³√5 

                           pois 2⁹√5³ = 2^9:3√5^3:3 =2³√5 

                     5√18+2√2 = 15√2 + 2√2 = (15+2)√2 = 17√2

                           pois 5√18 = 5√(3² ´2) = 5√3²´√2 = 5´3√2 = 15√2

                              

Passagem de um  fator para fora de um radical  

             

Decompõe-se o radicando num produto de factores primos e aplica-se a propriedade da multiplicação de radicais.Para passar um factor para dentro do radical eleva-se este ao índice do radical.

  Exemplos:

                    √108

108|   2

  54 |  2

  27|  3

    9| 3

     3| 3

  1|

então  √108 = √ (2²´3²´3) = √2²´√3³´√3 = 2´3´√3 = 6√3

                    2√5 = √(2²´5) = √20

                    3³√5² = ³√(3³´5²) = ³√(27´25) = ³√675

         

Potência de um radical

             

A potência de um radical tem a forma  (ⁿ√a)^p = ⁿ√(a^p) com a>o e n, p ∈ℕ.

                  

Exemplos:

                           (⁶√2)⁵ = ⁶√2⁵

         

 Radical de um radical

            

  É da forma ⁿ√(^p√a )= ^np√a com a>o e n, p ∈ℕ

                  

Exemplos:

                          ⁵√(√3) = ^2´5√3 = ¹⁰√3

Fonte: www.mundovestibular.com.br

            www.educaçao.uol.com.br
            http://www.educ.fc.ul.pt/

Questões sobre radiciação e racionalização de denominadores

01. (UFCE) Simplificar a expressão:

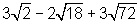
Solução:

Exercício simples que se baseia na decomposição em fatores primos de cada radicando e da utilização da propriedade P1, como você pode observar no detalhamento a seguir. Tenha em conta que na soma ou subtração de radicais, cada parcela deve ser considerada isoladamente para se obter o resultado de uma expressão. Ou seja, não se aplica que a soma de duas raízes de mesmo índice é igual a raiz da soma, como é o caso do produto, por exemplo.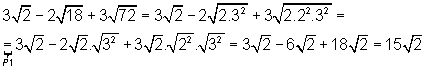

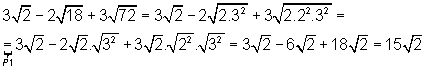
02. Calcular o quociente:

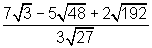
Solução:

Outro exercício de solução simples onde demonstro o uso das propriedades P1 e P3, e novamente, faço uso da decomposição em fatores primos dos radicandos:

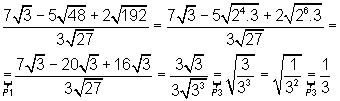
03. Escrever em ordem de grandeza crescente os radicais:

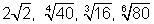
Solução:

Para fazer a comparação entre os radicais devemos, inicialmente, reduzí-los ao mesmo índice. Isto é feito calculando o mínimo múltiplo comum (mmc) dos índices e, após, aplicando a propriedade P6. O mmc(2, 4, 3, 6) = 12 e reescrevendo os radicais (P6) vem:

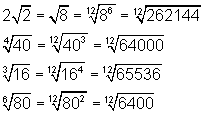
Agora, basta considerar a ordem dos radicandos para estabelecer a ordem crescente dos radicais:

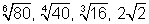
04. Efetuar

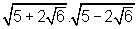
Solução:

Esboçada a seguir, onde utilizamos o fato de que o produto da soma pela diferença de dois números é igual ao quadrado do primeiro menos o quadrado do segundo (produto notável – PN) e as propriedades da Radiciação indicadas:

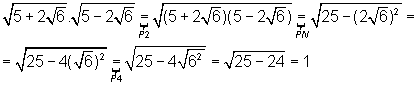
05. Simplifique a expressão:

 

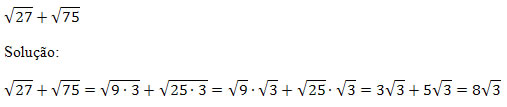
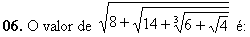
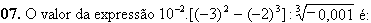
a) -0,1

b) -1,7

c) -17

d) 0,1

e) 1,7

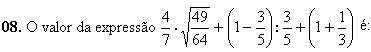
a) 0,4

b) 2,5

c) a

d) 1,5

e) 1

09. Escreva simplificadamente:

a) 

b)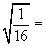 

c)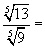 

10) Calcule .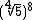

11)  Calcule .

12) Simplifique o radical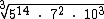 

13) (F. C. Chagas-SP) O número  √2352 corresponde a: 

a) 4  √7 . 
b) 4  √21 . 
c) 28  √3 . 
d) 28  √21 . 
e) 56  √3 .

14) (UFSC) O valor de  x, que satisfaz a equação  22x + 1 – 3 . 2x + 2 = 32, é:

15) (Fuvest)    é igual a:

16) (UFSC)  Dê o somatório da(s) proposição(ões) VERDADEIRA(S).

Gabarito:

06) A  07) B  08) B  09)  a)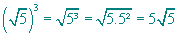 

b) 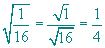          c)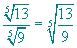    

10) 25     11) 49    12) 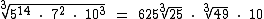   14) x = 3   15) E
16) 2 + 8 + 16 + 64 = 90