Conjunto dos Números Naturais (IN)
Um subconjunto importante de IN é o conjunto IN*:
IN*={1, 2, 3, 4, 5,...} ► o zero foi excluído do conjunto IN.
· Conjunto dos números inteiros (Z)
O conjunto IN é subconjunto de Z.
Temos também outros subconjuntos de Z:
Z* = Z-{0}
Z+ = conjunto dos inteiros não negativos = {0,1,2,3,4,5,...}
Z_ = conjunto dos inteiros não positivos = {0,-1,-2,-3,-4,-5,...}
Observe que Z+ = IN.
Podemos considerar os números inteiros ordenados sobre uma reta, conforme mostra o gráfico abaixo:
· Conjunto dos números racionais (Q)
Os números racionais são todos aqueles que podem ser colocados na forma de fração (com o numerador e denominador 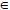 Z). Ou seja, o conjunto dos números racionais é a união do conjunto dos números inteiros com as frações positivas e negativas.
Z). Ou seja, o conjunto dos números racionais é a união do conjunto dos números inteiros com as frações positivas e negativas.
Então: 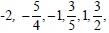 por exemplo, são números racionais.
por exemplo, são números racionais.
Exemplos:
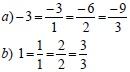
Assim, podemos escrever:
É interessante considerar a representação decimal de um número racional 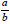 , que se obtém dividindo a por b.
, que se obtém dividindo a por b.
Exemplos referentes às decimais exatas ou finitas.
Exemplos referentes às decimais periódicas ou infinitas:
Toda decimal exata ou periódica pode ser representada na forma de número racional.
· Conjunto dos números irracionais
Os números irracionais são decimais infinitas não periódicas, ou seja, os números que não podem ser escrito na forma de fração (divisão de dois inteiros). Como exemplo de números irracionais, temos a raiz quadrada de 2 e a raiz quadrada de 3:
· Conjunto dos números reais (IR)
Dados os conjuntos dos números racionais (Q) e dos irracionais, definimos o conjunto dos números reais como:
O diagrama abaixo mostra a relação entre os conjuntos numéricos:

Portanto, os números naturais, inteiros, racionais e irracionais são todos números reais. Como subconjuntos importantes de IR temos:
IR* = IR-{0}
IR+ = conjunto dos números reais não negativo
IR_ = conjunto dos números reais não positivos
Obs: entre dois números inteiros existem infinitos números reais. Por exemplo:
- Entre os números 1 e 2 existem infinitos números reais:
1,01 ; 1,001 ; 1,0001 ; 1,1 ; 1,2 ; 1,5 ; 1,99 ; 1,999 ; 1,9999 ...
- Entre os números 5 e 6 existem infinitos números reais:
5,01 ; 5,02 ; 5,05 ; 5,1 ; 5,2 ; 5,5 ; 5,99 ; 5,999 ; 5,9999 ...
Operações com Conjuntos
Interseção
Os elementos que fazem parte do conjunto interseção são os elementos comuns aos conjuntos relacionados.
Exemplo 1:
Dados dois conjuntos A = {5,6,9,8} e B = {0,1,2,3,4,5}, se pedimos a interseção deles teremos:
A ∩ B = {5}, dizemos que A “inter” B é igual a 5.
Exemplo 2:
Dados os conjuntos B = {-3, -4, -5, -6} e C = {-7, -8, -9}, se pedirmos a interseção deles teremos:
B ∩ C = { } ou B ∩ C =
Exemplo 3:
Dados os conjuntos D = {1,2,3,4,5} e E = {3,4,5}. A interseção dos conjuntos ficaria assim:
E ∩ D = {3,4,5} ou E ∩ D = E, pode ser concluído também que
E
.jpg)
UniãoConjunto união são todos os elementos dos conjuntos relacionados.
Exemplo 1:
Dados os conjuntos A = { x | x é inteiro e -1 < x < 2} e B = {1,2,3,4} a união desses dois conjuntos é :
A U B = {0,1,2,3,4}
Exemplo 2:
Dados os conjuntos A = {1,2,3} e B = {1,2,3,4,5} a união desses conjuntos é:
A U B = {1,2,3,4,5}, nesse caso podemos dizer que A U B = B.
Diferença entre dois conjuntos.
Dados dois conjuntos A e B chama-se conjunto diferença ou diferença entre A e B o conjunto formado pelos elementos de A que não pertencem a B.
O conjunto diferença é representado por A – B.
Exemplo 1:
A = {1,2,3,4,5} e B = {3,4,5,6,7} a diferença dos conjuntos é:
A – B = {1,2}
Exemplo 2:
A = {1,2,3,4,5} e B = {8,9,10} a diferença dos conjuntos é:
A – B = {1,2,3,4,5}
Exemplo 3:
A = {1,2,3} e B = {1,2,3,4,5}a diferença dos conjuntos é:
A – B =
Exemplo 4:
Dados os conjuntos A = {1,2,3,4,5,6} e B = {5,6}, a diferença dos conjuntos é:
A – B = {1,2,3,4}. Como B
A – B =
Fonte: www.coladaweb.com.br
www.brasilescola.com
Exercícios sobre conjuntos numéricos
1) A quais conjuntos numéricos fundamentais não pertence o número 63 ?
Resolução:
Sabemos que 63 embora seja um número natural, não é um quadrado perfeito, nestas condições a sua raiz quadrada será um número irracional.
Também sabemos que 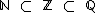 , que
, que 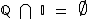 e que
e que 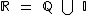 ou em outras palavras que, embora também sejam números reais, os números irracionais não são racionais, nem inteiros e nem naturais.
ou em outras palavras que, embora também sejam números reais, os números irracionais não são racionais, nem inteiros e nem naturais.
Logo:
2) ) Existe raiz quadrada de número primo que não seja irracional?
Resolução:
Vimos que a raiz quadrada de um número natural pode ser tanto natural, quanto irracional, mas para que a raiz seja natural, o número deve ser um quadrado perfeito.
Para que um número seja primo é preciso que além de natural ele possua exatamente apenas dois divisores distintos, o número um e ele próprio.
Falando em termos de conjuntos, a intersecção do conjunto dos números primos com o conjunto natural dos quadrados perfeitos é igual ao conjunto vazio ( 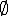 ), ou seja, um número primo não pode ser um quadrado perfeito e vice-versa.
), ou seja, um número primo não pode ser um quadrado perfeito e vice-versa.
Assim sendo:
Não existe raiz quadrada de número primo que não seja irracional.
3) Se a e b são números pertencentes a 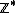 e
e 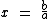 , a quais conjuntos numéricos fundamentais podemos afirmar com certeza que x pertence, quaisquer que sejam os valores de a e b?
, a quais conjuntos numéricos fundamentais podemos afirmar com certeza que x pertence, quaisquer que sejam os valores de a e b?
Resolução:
A partir do enunciado, podemos chamar de A o conjunto ao qual x pertence e representá-lo por 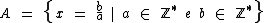
Sabemos que, dentre outras formas, podemos representar o conjunto dos números racionais por 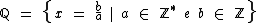
Como podemos observar, A é um subconjunto de 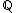 , isto é,
, isto é, 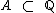
Sabemos também que 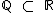
Assim sendo:
Podemos afirmar com certeza que 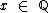 e
e 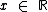 .
.
4) Se 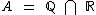 e
e 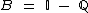 , tem-se que
, tem-se que 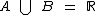 ?
?
Resolução:
A intersecção entre dois conjuntos onde um conjunto está contido no outro é o próprio conjunto que está contido, como 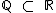 , temos que
, temos que 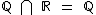 , logo
, logo 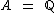
A diferença entre conjuntos difere da operação de intersecção. A diferença entre os conjuntos 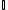 e
e 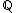 é o conjunto de todos os elementos que pertencem ao conjunto
é o conjunto de todos os elementos que pertencem ao conjunto 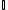 e que não pertencem ao conjunto
e que não pertencem ao conjunto 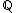 , que obviamente é o próprio
, que obviamente é o próprio 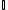 , pois em
, pois em 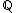 não há qualquer número irracional, logo
não há qualquer número irracional, logo 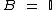
Então 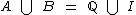 e como já aprendemos que
e como já aprendemos que 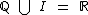 , temos que:
, temos que:
Sim, tem-se que 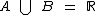 .
.
5) Assinale V ou F:
a) 5/4 E Q b) 1,888.... E Q c) 12 E Q
6) Classifique cada sentença como verdadeira (V) ou falsa (F):
a) A soma de um número racional com um número irracional é sempre um número racional.
b) O produto de dois números irracionais pode ser racional.
c) A soma de dois números irracionais é sempre um número irracional.
7) (FATEC) Sejam a e b números irracionais.
Dada as afirmações:
I) a.b é um número irracional.
II) a + b é um número irracional.
III) a - b pode ser um número racional.
Podemos concluir que:
a) as três são falsas.
b) as três são verdadeiras.
c) somente I e III são verdadeiras.
d) somente I é verdadeira.
e) somente I e II são falsas.
8) (CEFET - AL) Em relação aos principais conjuntos numéricos, é CORRETO afirmar que:
a) Todo número racional é natural, mas nem todo número natural é racional.
b) Todo número inteiro é natural, mas nem todo número natural é inteiro.
c) Todo número real é natural, mas nem todo número natural é real.
d) Todo número racional é inteiro, mas nem todo número inteiro é racional.
e) Todo número irracional é real.
9) (Fameca-SP) Se  ,
,  e
e  então,
então,  é:
é:
 ,
,  e
e  então,
então,  é:
é:
a) {0} b) {4} c) {0,4} d) {0,1,2,3,4} e) {0,1,2,3,4,5}
10) Dado os conjuntos A = {1, 2, 3} e B = {2, 3, 4, 5, 6} efetue:
a) L = A U B b) M = A ∩ B c) N = A – B d) O = B – A
Gabarito:
5) todas as proposições estão corretas. 6) a) V b) V c) F 7) E 8) E 9) C 10) a) A U B = {1, 2, 3, 4, 5, 6} b) A ∩ B = {2, 3} c) A - B = {1} d) B - A = {4, 5, 6}
Poderia esclarecer mais o gabarito, pois não está de bom entendimento.Obrigada pela atenção.
ResponderExcluir