O atual sistema financeiro utiliza o regime de juros compostos, pois ele oferece uma maior rentabilidade se comparado ao regime de juros simples, onde o valor dos rendimentos se torna fixo, e no caso do composto o juro incide mês a mês de acordo com o somatório acumulativo do capital com o rendimento mensal, isto é, prática do juro sobre juro. As modalidades de investimentos e financiamentos são calculadas de acordo com esse modelo de investimento, pois ele oferece um maior rendimento, originando mais lucro.
Considere que uma pessoa aplique R$ 500,00 durante 8 meses em um banco que paga 1% de juro ao mês. Qual será o valor ao final da aplicação?
A tabela demonstrará mês a mês a movimentação financeira na aplicação do regime de juros compostos.
.jpg)
No final do 8º mês o montante será de R$ 541,43.
Uma expressão matemática utilizada no cálculo dos juros compostos é a seguinte:
M = C * (1 + i)t, onde:
M: montante
C: capital
i: taxa de juros
t: tempo de aplicação
Obs.: Os cálculos envolvendo juros compostos exigem conhecimentos de manuseio de uma calculadora científica.
Exemplo 2
Qual o montante produzido por um capital de R$ 7.000,00 aplicados a uma taxa de juros mensais de 1,5% durante um ano?
C: R$ 7.000,00
i: 1,5% ao mês = 1,5/100 = 0,015
t: 1 ano = 12 meses
M = C * (1 + i)t
M = 7000 * (1 + 0,015)12
M = 7000 * (1,015)12
M = 7000 * 1,195618
M = 8369,33
O montante será de R$ 8.369,33.
Com a utilização dessa fórmula podemos também calcular o capital de acordo com o montante.
Exemplo 3
Calcule o valor do capital que, aplicado a uma taxa de 2% ao mês, rendeu em 10 meses a quantia de R$ 15.237,43?
M: R$ 15.237,43
t: 10
i: 2% a.m. = 2/100 = 0,02
M = C * (1 + i)t
15237,43 = C * (1 + 0,02)10
15237,43 = C * (1,02)10
15237,43 = C * 1,218994
C = 15237,43 / 1,218994
C = 12500,00
O capital é de R$ 12.500,00.
Questões propostas e resolvidas sobre juros compostos
1) Uma loja vende seus artigos nas seguintes condições: à vista com 30% de desconto sobre o preço da tabela ou no cartão de crédito com 10% de acréscimo sobre o preço de tabela. Um artigo que a vista sai por R$ 7.000,00 no cartão sairá por?
2) A quantia de R$ 15.000,00 é emprestada a uma taxa de juros de 20% ao mês. Aplicando-se JUROS COMPOSTOS, determine o valor que deverá ser pago para a quitação da dívida, três meses depois.
3) Um investidor aplicou R$ 500,00 em caderneta de poupança. As taxas de juros foram de 25% no primeiro mês e 28% no segundo mês.
Nessas condições, determine o valor acumulado, ao final desses dois meses.
4) Planejo emprestar R$ 18.000,00 por um período de 18 meses ao final do qual pretendo receber de volta um total de R$ 26.866,57. Qual deve ser o percentual da taxa de juro composto para que eu venha a conseguir este montante?
5) Um comprador pagou uma mercadoria em duas parcelas, sendo uma no ato da compra e a outra, trinta dias depois. Se o preço à vista era de R$ 430,00, o valor da primeira parcela foi R$ 230,00 e se lhe foi cobrada uma taxa de juros de 15% ao mês, determine o valor da segunda parcela.
6) A população de uma cidade, no final de 1998, era de 150 000 habitantes. Ela cresce 2% ao ano. Calcule o aumento da população dessa cidade do final de 1997 até o final do ano 2000.
7) Comprei o material para a reforma da minha casa, pelo qual pagarei um total de R$ 38.664,00. O seu valor à vista era de R$ 27.000,00 e a taxa de juros é de 2,4% a.m. Por quantos anos eu pagarei por este material?
8) Um aplicador investiu R$ 35.000,00 por 1 semestre, à taxa de juros simples de 24,72% a.a. Em quanto o capital foi aumentado por este investimento?
9) O valor principal de uma aplicação é de R$ 2.000,00. Resgatou-se um total de R$ 2.450,00 após 1 mês. Qual o valor da taxa de juros a.d.?
10) Nas operações de empréstimo, uma financeira cobra taxa efetiva de juros, no regime de capitalização composta, de 10,25% ao ano. Isso equivale a cobrar juros com taxa anual e capitalização semestral de
A) 10,51% B) 10,25% C) 5% D) 10% E) 5,51%
Agora algumas questões resolvidas sobre juros compostos
11) Uma pessoa caminha em uma pista plana com a forma de triângulo retângulo. Ao dar uma volta completa na pista com velocidade constante de caminhada, ela percorre 600 e 800 metros nos trajetos correspondentes aos catetos da pista triangular, e o restante da caminhada ela completa em 10 minutos. A velocidade constante de caminhada dessa pessoa é igual a quantos quilômetros por hora?
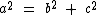
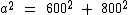
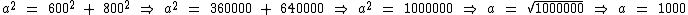
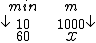
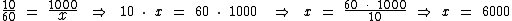
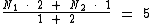
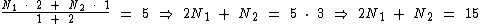
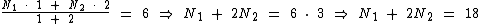
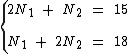
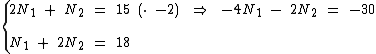
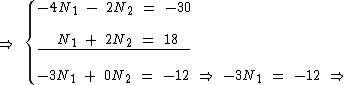
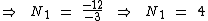
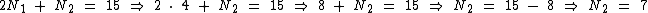
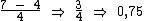
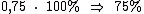
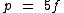
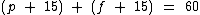
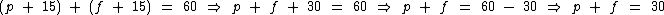
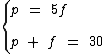
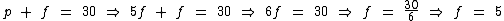
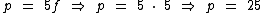
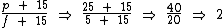
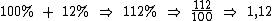
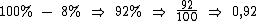
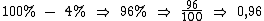
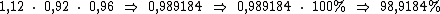
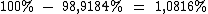
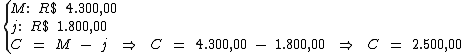
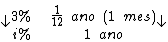
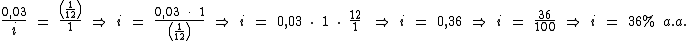
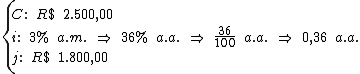
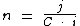
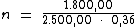
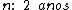
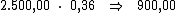
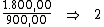
7) Comprei o material para a reforma da minha casa, pelo qual pagarei um total de R$ 38.664,00. O seu valor à vista era de R$ 27.000,00 e a taxa de juros é de 2,4% a.m. Por quantos anos eu pagarei por este material?
8) Um aplicador investiu R$ 35.000,00 por 1 semestre, à taxa de juros simples de 24,72% a.a. Em quanto o capital foi aumentado por este investimento?
9) O valor principal de uma aplicação é de R$ 2.000,00. Resgatou-se um total de R$ 2.450,00 após 1 mês. Qual o valor da taxa de juros a.d.?
10) Nas operações de empréstimo, uma financeira cobra taxa efetiva de juros, no regime de capitalização composta, de 10,25% ao ano. Isso equivale a cobrar juros com taxa anual e capitalização semestral de
A) 10,51% B) 10,25% C) 5% D) 10% E) 5,51%
Agora algumas questões resolvidas sobre juros compostos
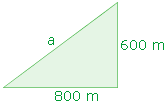
11) Uma pessoa caminha em uma pista plana com a forma de triângulo retângulo. Ao dar uma volta completa na pista com velocidade constante de caminhada, ela percorre 600 e 800 metros nos trajetos correspondentes aos catetos da pista triangular, e o restante da caminhada ela completa em 10 minutos. A velocidade constante de caminhada dessa pessoa é igual a quantos quilômetros por hora?
A resolução desta questão se baseia no teorema de Pitágoras. Vamos descobrir a medida do trajeto percorrido em 10 minutos, a partir do qual iremos calcular a velocidade procurada.

Para solucionar o problema vamos observar a figura ao lado que representa a pista em questão.
Em função do enunciado sabemos que o lado a, correspondente à hipotenusa, foi percorrido em 10 minutos, assim sendo, basta descobrirmos o seu comprimento para podermos calcular a velocidade na qual ele foi percorrido, que é constante em todo o percurso.
Segundo o teorema de Pitágoras o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos, para quaisquer triângulos retângulos.
O teorema pode ser representado pela seguinte equação:
Neste nosso problema temos b = 600 e c = 800, o que nos leva à seguinte equação:
Agora temos condições de descobrir quantos metros possui o trecho da pista que foi percorrido em dez minutos.
Vejamos:
Agora sabemos o trecho percorrido em dez minutos tem 1000 m de comprimento.
Se em 10 min percorremos 1000 m, em 60 min (ou seja, em 1 h) vamos percorrer quantos metros?
Resolvendo a regra de três simples e direta temos:
Então a velocidade constante de caminhada foi de 6000 m por hora, mas o enunciado pede a velocidade em km/h, por isto precisamos realizar mais uma conversão, agora de m para km.
Já aprendemos que a conversão de metros para quilômetros é realizada dividindo-se por 1000 a medida em metros. Como temos 6000 metros, ao dividi-los por 1000 obtemos 6 quilômetros.
Portanto:
A velocidade constante de caminhada é de 6 km/h.
12) Um professor aplicou duas provas, cada uma valendo 10. O combinado com seus alunos era que a média final de cada um seria calculada utilizando-se peso 1 na nota da primeira prova e peso 2 na nota da segunda prova. Na hora de fazer os cálculos da média de um aluno, o professor trocou os pesos entre as duas provas, obtendo média igual a 5. Corrigido o erro, a média do aluno subiu 1 ponto. Nas condições do problema, a nota que esse aluno tirou na segunda prova superou sua nota da primeira prova em quantos por cento?
A resolução desta outra questão envolve tanto o cálculo da média aritmética ponderada, quanto o cálculo de porcentagem.
Em resumo precisamos descobrir o valor de cada nota, para então descobrimos quantos por cento a segunda nota é maior que a primeira. Vamos então à resolução.
Segundo o enunciado, erroneamente a média foi calculada com os pesos invertidos. A primeira nota tendo peso 2e a segunda peso 1:
No entanto a média deveria ser calculada tendo a primeira nota peso 1 e a segunda peso 2:
Note que com os pesos corretos a média passou de 5 a 6 conforme o enunciado.
Vamos tratar as equações eliminado assim as frações:
Como temos duas variáveis com duas equações, vamos montar um sistema de equações com duas variáveis para identificarmos o valor de cada nota obtida pelo aluno:
Vamos eliminar N2 multiplicando a primeira equação por -2 e somando à segunda equação, obtendo assim o valor de N1:
Agora podemos obter o valor de N2 substituindo N1 pelo seu valor na primeira equação:
Agora sabemos que o aluno teve nota 4 na primeira prova e nota 7 na segunda prova.
Como o enunciado pergunta quantos por cento a segunda nota é maior que a primeira, precisamos dividir a diferença entre a segunda e a primeira, pela primeira nota:
Esta divisão resulta em 0,75 que é o valor procurado, mas na forma decimal, precisamos então multiplicá-lo por100% para convertê-lo na forma percentual:
Então:
A nota que esse aluno tirou na segunda prova superou sua nota da primeira prova em 75%.
13) Hoje, a idade de um pai é o quíntuplo da idade de seu filho e, daqui a 15 anos, a soma das idades será de 60 anos. Pode-se afirmar que daqui a 15 anos, a idade do pai será quantas vezes a idade do filho?
Nesta questão iremos montar um sistema de equações do primeiro grau com duas incógnitas para obtermos a idade do pai e a idade do filho, depois iremos utilizar o conceito de razão para descobrirmos quantas vezes a primeira é maior que a última.
A idade do pai é o quíntuplo da idade do seu filho, o que nos leva à seguinte equação:
Onde p é a idade do pai e f a idade do filho.
Daqui a 15 anos a soma das idades será de 60 anos. Isto pode ser expresso como:
Para ficar mais simples o trabalho, vamos simplificar a expressão:
Vamos então montar o sistema de equações:
Vamos solucioná-lo pelo método da substituição. Na segunda equação vamos substituir p por 5f:
Agora podemos substituir f por 5 na primeira equação:
Sabendo que o pai tem 25 anos e que o filho tem 5 anos, basta calcularmos a razão das idades que eles terão daqui quinze anos:
Então:
Daqui a 15 anos, a idade do pai será 2 vezes a idade do filho.
14) Suponha que o preço da ação de uma empresa tenha sofrido as seguintes variações sucessivas no primeiro trimestre de um determinado ano: em janeiro, aumentou 12%; em fevereiro, sofreu uma redução de 8%; e, em março, uma redução de 4%, sempre em relação ao mês anterior. Considerando-se essas variações, ao final do trimestre, em relação ao preço original, o preço da ação subiu ou desceu quanto por cento aproximadamente (sem casas decimais)?
Resolvemos esta questão através do cálculo em sequência de porcentagens.
Quando queremos acrescentar 12% a um valor, devemos multiplicá-lo por 1,12:
O 100% se refere ao valor original e o 12% se refere ao acréscimo.
Para reduzirmos 8% precisamos multiplicar por 0,92:
A redução de 4% é realizada da mesma forma multiplicando por 0,96:
Multiplicando estes três percentuais na forma decimal iremos descobrir se o valor da ação aumentou, diminui, ou se manteve o mesmo:
Como 98,9184% é inferior a 100%, isto indica que o valor da ação diminui.
Obtemos a variação percentual calculando a diferença:
Portanto:
O preço da ação desceu aproximadamente 1%.
15) Comprei um novo computador, mas como não tinha o dinheiro todo, fiz um empréstimo para pagá-lo. Ao final do empréstimo terei pago R$ 4.300,00. Só de juros pagarei R$ 1.800,00. A taxa foi de 3% a.m. Por quantos anos pagarei pelo empréstimo? Qual o preço do computador sem os juros?
Primeiramente iremos calcular o valor do capital.
A diferença entre o montante (R$ 4.300,00) e o valor total do juro (R$ 1.800,00), nos dá o valor do capital:
Veja que neste caso a taxa de juros e o período não estão na mesma unidade de tempo. Neste caso, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
Resolvendo:
Identificando-se os termos disponíveis, temos:
Para calcularmos o período de tempo utilizaremos a fórmula:
Substituindo o valor dos termos temos:
Logo:
Portanto:
O valor do computador sem os juros era de R$ 2.500,00 e o prazo de pagamento foi de 2 anos.
Sem utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, pelo seguinte raciocínio:
Ao multiplicarmos o valor do capital pela taxa de juros, iremos obter o juro referente a cada período:
Neste caso, basta-nos dividir o valor de R$ 1.800,00, referente ao valor total do juro, por R$ 900,00 correspondente ao valor do juro em cada período, obtendo assim o período de tempo procurado:
16) Aninha retirou de uma aplicação o total R$ 74.932,00, após decorridos 3,5 semestres. O valor dos juros obtidos foi de R$ 22.932,00. Qual a taxa de juros a.b.?
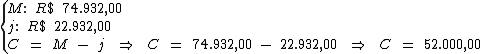
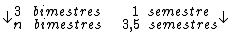
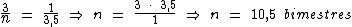
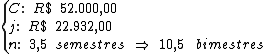
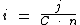
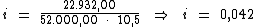
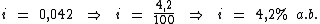
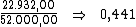
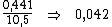
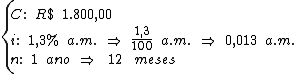

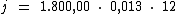
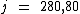
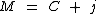
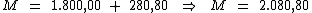
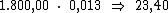
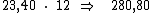
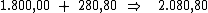
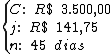
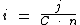
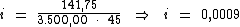
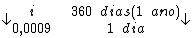
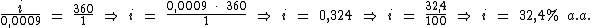
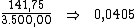
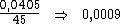
19) Um aparelho DVD Player foi pago em 5 prestações mensais de R$ 383,90 sem entrada. Sabendo-se que a taxa de juros foi de 2% a.m., qual seria o pago caso eu tivesse feito a compra à vista?
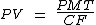
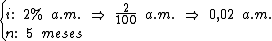
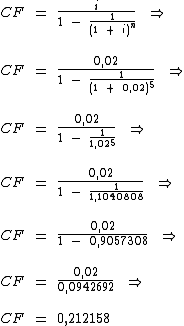
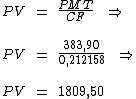
20) Aplicando-se R$ 15.000,00 a uma taxa de juro composto de 1,7% a.m., quanto receberei de volta após um ano de aplicação? Qual o juro obtido neste período?
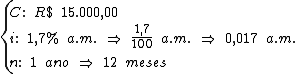

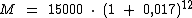

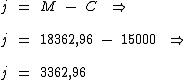
Inicialmente o valor do capital será obtido subtraindo-se do montante (R$ 74.932,00), o valor total do juro (R$ 22.932,00):
Veja bem que neste caso a taxa de juros e o período não estão na mesma unidade de tempo. Sendo assim, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
Resolvendo:
Identificando-se os termos disponíveis, temos:
Para calcularmos a taxa de juros utilizaremos a fórmula:
Substituindo o valor dos termos temos:
Logo:
Portanto:
4,2% a.b. é a taxa de juros da aplicação na qual Aninha investiu.
Alternativamente poderíamos dividir o valor total dos juros, R$ 22.932,00, pelo valor do principal, R$ 52.000,00, de sorte a encontrar a taxa de juros total do período:
Dividindo-se então, esta taxa de 0,441 pelo período de tempo, 10,5, obteríamos a taxa desejada:
17) Timóteo pagou mensalmente, pelo período de 1 ano, por um curso que à vista custava R$ 1.800,00. Por não ter o dinheiro, financiou-o a uma taxa de juros simples de 1,3% a.m. Qual o valor total pago pelo curso? Qual o valor dos juros?
Veja que neste caso a taxa de juros e o período não estão na mesma unidade de tempo. Neste caso, devemos converter uma das unidades.
Identificando-se os termos disponíveis, temos:
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
Logo:
O montante é obtido somando-se ao valor do capital, o valor total dos juros. Tal como na fórmula:
Ao substituirmos o valor dos termos temos:
Portanto:
O valor dos juros foi de R$ 280,80, que acrescentado ao preço do curso de R$ 1.800,00, totalizou R$ 2.080,80.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o valor do capital pela taxa de juros. Então o valor do juro por período seria:
Ora, sendo o valor do juro em cada período correspondente a R$ 23,40, resta-nos multiplicar este valor por 12, correspondente ao período de tempo, para termos o valor procurado:
O valor do montante será encontrado, simplesmente somando-se ao valor do principal, o valor total dos juros:
18) Em uma aplicação recebi de juros R$ 141,75. O dinheiro ficou aplicado por 45 dias. Eu tinha aplicado R$ 3.500,00. Qual foi a taxa de juros a.a. da aplicação?
Identificando-se os termos disponíveis, temos:
Para calcularmos a taxa de juros utilizaremos a fórmula:
Substituindo o valor dos termos temos:
No entanto, como a unidade de tempo da taxa solicitada está em anos ('a.a.') e o cálculo foi realizado na unidade do período de tempo que está em 'dias', devemos converter a unidade de tempo da taxa calculada de a.d. ('dias') para a.a. ('anos').
Logo:
Resolvendo:
Portanto:
32,4% a.a. foi a taxa de juros simples da aplicação.
Alternativamente poderíamos dividir o valor total dos juros, R$ 141,75, pelo valor do principal, R$ 3.500,00, de forma a encontrar a taxa de juros total do período:
Dividindo-se então, esta taxa de 0,0405 pelo período de tempo, 45, obteríamos a taxa desejada:
Resta ainda converter a taxa de juros para a unidade de tempo solicitada, o que pode ser feito se realizando o procedimento de conversão conforme efetuado acima.
Para o cálculo de PV que corresponde ao valor à vista, utilizaremos a fórmula:
Para calcularmos o coeficiente de financiamento utilizaremos as variáveis a seguir:
Vamos então calculá-lo:
Sabendo-se que PMT = 383,90 e que CF = 0,212158, podemos calcular PV:
Portanto:
Eu teria pago um total de R$ 1.809,50 se tivesse realizado a compra à vista.
Primeiramente vamos identificar cada uma das variáveis fornecidas pelo enunciado do problema:
Como a taxa de juros está em meses, também iremos trabalhar com o período de tempo em meses e não em anos como está no enunciado do problema.
Pelo enunciado identificamos que foram solicitados o montante e o juro, utilizaremos, portanto a fórmula abaixo que nos dá o montante:
Ao substituirmos cada uma das variáveis pelo seu respectivo valor teremos:
Podemos então realizar os cálculos para encontramos o valor do montante:
Logo o montante a receber será de R$ 18.362,96. Sabemos que a diferença entre o montante e o capital aplicado nos dará os juros do período. Temos então:
Portanto:
Após um ano de aplicação receberei de volta um total de R$ 18.362,96, dos quais R$ 3.362,96 serão recebidos a título de juros.
Gabarito:
1) R$ 11.000,00 2) R$ 25.900,00 3) R$ 800,00 4) i = 2,25% 5) R$ 230,00 6) 9 000 habitantes aproximadamente. 7) 1,5 anos 8) R$ 4.326,00 9) 0,75% A.D 10) D
Nenhum comentário:
Postar um comentário