Função exponencial exercícios e teoria

Função exponencial

Uma função  dada por , em que em que a é constante positiva e diferente de 1, denomina-se função exponencial.

A função exponencial será crescente quando a base a for maior que 1, e decrescente se a for positivo menor que 1. Seu gráfico terá sempre um do seguintes aspectos:

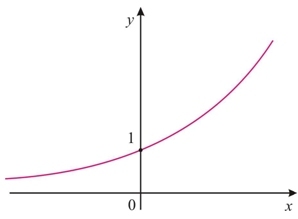
a > 1, f é crescente

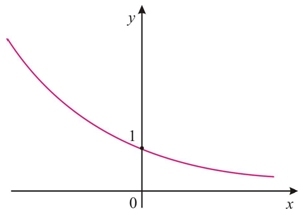
a < 1, f é decrescente

Observe que nos dois casos, o gráfico de F(x) = a^x não cruza o eixo Ox, pois para  para qualquer . No entanto o gráfico de uma função  cruza o eixo Oy no ponto (0,1), pois a⁰ = 1.

O domínio da função exponencial é D=R, e seu contradomínio é CD=R positivos com exceção do numero 0. Como a > 0 e a ≠ 1, as imagens da função sempre serão positivas.

Outra característica da função exponencial é ela ser bijetora, pois f é sobrejetora e injetora.

Representação da Função Exponencial no Plano Cartesiano

Para representarmos graficamente uma função exponencial, podemos fazê-lo da mesma forma que fizemos com a função quadrática, ou seja, arbitrarmos alguns valores para x, montarmos uma tabela com os respectivos valores de f(x), localizarmos os pontos no plano cartesiano e traçarmos a curva do gráfico.

Para a representação gráfica da função 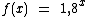 arbitraremos os seguinte valores para x:

-6, -3, -1, 0, 1 e 2.

Montando a tabela temos:

x	y = 1,8x
-6	y = 1,8-6 = 0.03
-3	y = 1,8-3 = 0.17
-1	y = 1,8-1 = 0.56
0	y = 1,80 = 1
1	y = 1,81 = 1.8
2	y = 1,82 = 3.24

Ao lado temos o gráfico desta função exponencial, onde localizamos cada um dos pontos obtidos da tabela e os interligamos através da curva da função: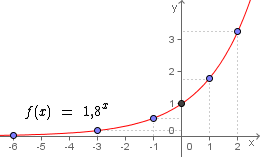

Fonte: www.Infoescola.com
           www.brasilescola.com
           www.matematicadidatica.com.br

Exercícios sobre função exponencial

1) (Vunesp) - Uma certa substância se decompõe aproximadamente segundo a lei , em que K é uma constante, t indica o tempo em minutos e Q(t) indica a quantidade da substância, em gramas, no instante t. Considerando os dados desse processo de decomposição mostrados no gráfico, determine os valores de K e de a.


Resolução:

A função exponencial  passa pelos pontos (a, 512) e (0, 2048).
Substituindo esses pontos na função, temos:

2) (PUC/MG - adaptada) - O número de bactérias em um meio duplica de hora em hora. Se, inicialmente, existem 8 bactérias no meio, ao fim de 10 horas o número de bactérias será:



Resolução:

No tempo t = 0, o número de bactérias é igual a 8.
No tempo t = 1, o número de bactérias é dado por 8.2 = 16.
No tempo t = 2, o número de bactérias é dado por 8.2.2 = 32.
Assim, no tempo t = x, o número de bactérias é dada por .
Logo, no tempo desejado, ou seja, ao fim de 10 horas, o número de bactérias será de .

Resposta: E.

3) (Unit-SE) Uma determinada máquina industrial se deprecia de tal forma que seu valor, t anos após a sua compra, é dado por v(t) = v₀ * 2 ^–0,2t, em que v₀ é uma constante real. Se, após 10 anos, a máquina estiver valendo R$ 12 000,00, determine o valor que ela foi comprada.

Temos que v(10) = 12 000, então:

v(10) = v0 * 2 ^–0,2*10
12 000 = v0 * 2 ^–2
12 000 = v0 * 1/4

12 000 : 1/ 4 = v0

v0 = 12 000 * 4

v0 = 48 000

A máquina foi comprada pelo valor de R$ 48 000,00.

4) (EU-PI) Suponha que, em 2003, o PIB (Produto Interno Bruto) de um país seja de 500 bilhões de dólares. Se o PIB crescer 3% ao ano, de forma cumulativa, qual será o PIB do país em 2023, dado em bilhões de dólares? Use 1,03²⁰ = 1,80.

Temos a seguinte função exponencial:

P(x) = P0 * (1 + i)^t

P(x) = 500 * (1 + 0,03)²⁰

P(x) = 500 * 1,03²⁰

P(x) = 500 * 1,80

P(x) = 900

O PIB do país no ano de 2023 será igual a R$ 900 bilhões.

5)  (Fatec-SP - Adaptada) Suponhamos que a população de uma certa cidade seja estimada, para daqui a x anos, por  . Determine a população referente ao terceiro ano.

  A população referente ao 3º ano é de 19.875 habitantes.

6)  Qual o domínio da função exponencial  y = 2^x ?

Resolução:

Sabemos que o domínio de uma função y = f(x) é o conjunto de valores que podem ser atribuídos a x. Observe que x sendo um expoente, ele poderá assumir qualquer valor e, portanto, o domínio da função dada é o conjunto dos números reais, ou seja: 
D = R.

 

7) Dada a função exponencial, calcule o valor de m que a torne decrescente.

Resolução:

Para que a função   seja decrescente os possíveis valores de m deve respeitar a seguinte condição: 5 < m < 5,5. Portanto:
S = {m Є R / 5 < m < 5,5}
 
8) Na função exponencial a seguir calcule o valor de k, considerando uma função crescente.
 

Resolução:

A condição para que uma função exponencial seja crescente é considerar a base do expoente x maior que 1.

12 – 2k > 1
12 > 2k
k < 6

A função exponencial f(x) = (12 – 2k)x é crescente quando k < 6.

9)  (Unicamp, 2011) Em uma xícara que já contém certa quantidade de açúcar, despeja-se café. A curva abaixo representa a função exponencial M(t), que fornece a quantidade de açúcar não dissolvido (em gramas), t minutos após o café ser despejado. Pelo gráfico, podemos concluir que

a) M(t) = 2^4−t/75
b) M(t) = 2^4−t/50
c) M(t) = 2^5−t/50
d) M(t) = 2^5−t/150

Resolução

• Para o ponto (0,16), temos:

M(0) = 16 = 2⁴

• Para o ponto (150,4), temos:

M(150) = 4 = 2² = M(0).2^k = 2⁴.2^k = 2^{4 + k} = 2^{4 - 2} = 2^{4 - 150/75} 

M(t) = 2^{4 - t/75}

10) (PUCC-SP) Numa certa cidade, o número de habitantes, num raio de r jm a partir do seu centro é dado por P(r) = k * 2^3r, em que k é constante e r > 0. Se há 98 304 habitantes num raio de 5 km do centro, quantos habitantes há num raio de 3 km do centro?

Resolução:

P(r) = k * 2^3r

98 304 = k * 2 ^3*5

98 304 = k * 215

98 304 = k * 32 768

k =98 304 / 32 768

k = 3

Calculando o número de habitantes num raio de  3 km

P (r) = k * 2^3r

P (3) = 3 * 2^3*3

P (3) = 3 * 29

P (3) = 3 * 512

P(3) = 1536

O número de habitantes num raio de 3 km é igual a 1536.

11) (LUMEN) O maior valor inteiro que devemos atribuir a "p" para que a função f(x) = (11 - p)x seja crescente é: 

a)8 
b)9 
c)7 
d)10 
e)11 

12) (ITA) Considere a função f : Z \ {0} --> R,,x para quais y² + 2y + f(x) = 0 tem raiz dupla é: 

a)Zero 
b)6 
c)2 
d)1 
e)4 

13) (UFPB) O valor de um certo imóvel, em reais, daqui a t anos é dado pela função V(t) = 1000(0,8)t . Daqui a dois anos, esse imóvel sofrerá, em relação ao valor atual, uma desvalorização de: 

a)R$ 800,00 
b)R$ 512,00 
c)R$ 640,00 
d)R$ 360,00 
e)R$ 200,00 

14) As funções y = a^x e y = b^x com a > 0 e b > 0 e a b têm gráficos que se interceptam em:

a) nenhum ponto;
b) 2 pontos;
c) 4 pontos;
d) 1 ponto;
e) infinitos pontos.

15) (U. E. FEIRA DE SANTANA - BA) O gráfico da função real f(x) = x² - 2:

a) intercepta o eixo dos x no ponto (1, 0);
b) intercepta o eixo dos x no ponto (0, 1);
c) intercepta o eixo dos x no ponto (2, 0);
d) intercepta o eixo dos x no ponto (0, -2);
e) não intercepta o eixo dos x.

16) (FIC / FACEM) A produção de uma indústria vem diminuindo ano a ano. Num certo ano, ela produziu mil unidades de seu principal produto. A partir daí, a produção anual passou a seguir a lei y = 1000 . (0,9)^x. O número de unidades produzidas no segundo ano desse período recessivo foi de:

a) 900
b) 1000
c) 180
d) 810
e) 90

17) (ENEM-2009) A população mundial está ficando mais velha, os índices de natalidade diminuíram e a expectativa de vida aumentou. No gráfico seguinte, são apresentados dados obtidos por pesquisa realizada pela Organização das Nações Unidas (ONU), a respeito da quantidade de pessoas com 60 anos ou mais em todo o mundo. Os números da coluna da direita representam as faixas percentuais. Por exemplo, em 1950 havia 95 milhões de pessoas com 60 anos ou mais nos países desenvolvidos, número entre 10% e 15% da população total nos países desenvolvidos.

Suponha que o modelo exponencial y = 363e^0,03x, em que x = 0 corresponde ao ano 2000, x = 1 corresponde ao ano 2001, e assim sucessivamente, e que y é a população em milhões de habitantes no ano x, seja usado para estimar essa população com 60 anos ou mais de idade nos países em desenvolvimento entre 2010 e 2050. Desse modo, considerando e^0,3 = 1,35, estima-se que a população com 60 anos ou mais estará, em 2030, entre

A) 490 e 510 milhões.

B) 550 e 620 milhões.

C) 780 e 800 milhões.

D) 810 e 860 milhões.

E) 870 e 910 milhões.

RESOLUÇÃO:

Veja que o enunciado contém muitas informações que não serão úteis. Vamos focar apenas na pergunta do problema. Precisamos apenas calcular a população com 60 anos ou mais em 2030.

Observe que de 2000 até 2030 terão se passado 30 anos. Agora basta substituir na função y = 363e^0,03x.

Portanto o gabarito será letra E.

18) Considere que uma pessoa decida investir uma determinada quantia e que lhe sejam apresentadas três possibilidades de investimento, com rentabilidades líquidas garantidas pelo período de um ano, conforme descritas:

Investimento A: 3% ao mês

Investimento B: 36% ao ano

Investimento C: 18% ao semestre

As rentabilidades, para esses investimentos, incidem sobre o valor do período anterior. O quadro fornece algumas aproximações para a análise das rentabilidades:

Para escolher o investimento com a maior rentabilidade anual, essa pessoa deverá

A) escolher qualquer um dos investimentos A, B ou C, pois as suas rentabilidades anuais são iguais a 36%.

B) escolher os investimentos A ou C, pois suas rentabilidades anuais são iguais a 39%.

C) escolher o investimento A, pois a sua rentabilidade anual é maior que as rentabilidades anuais dos investimentos B e C.

D) escolher o investimento B, pois sua rentabilidade de 36% é maior que as rentabilidades de 3% do investimento A e de 18% do investimento C.

E) escolher o investimento C, pois sua rentabilidade de 39% ao ano é maior que a rentabilidade de 36% ao ano dos investimentos A e B.

RESOLUÇÃO:

Galera, vamos calcular quanto vai render cada um dos investimentos.

→ Investimento A: Rende  3% ao mês.

100% + 3% =103% = 1,03

Durante 12 meses teremos 1,03¹² = 1,426 do valor inicial. (consulte a tabela)

→ Investimento B: Rende  36% ao ano.

100% + 36% =136% = 1,36

Durante 1 ano teremos 1,36 do valor inicial.

→ Investimento C: Rende  18% ao semestre.

100% + 18% =118% = 1,18

Durante 2 semestres teremos 1,18² = 1,3924 do valor inicial

Portanto, o investimento de maior rentabilidade no ano é o  Investimento A. Gabarito letra C.

Gabarito:

          11) B  12) C  13) D  14) D  15) A  16) D