Artigo sobre arranjo simples e com elementos repetidos com exemplos e questões de vestibulares para um melhor aprendizado.
Arranjo simples
Arranjo simples
Arranjo simples de  elementos tomados
elementos tomados  a
a  , onde
, onde 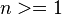 e
e  é um número natural, é qualquer ordenação de
é um número natural, é qualquer ordenação de  elementos dentre os
elementos dentre os  elementos, em que cada maneira de tomar os elementos se diferenciam pela ordem e natureza dos elementos.
elementos, em que cada maneira de tomar os elementos se diferenciam pela ordem e natureza dos elementos.
 elementos tomados
elementos tomados  a
a  , onde
, onde 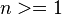 e
e  é um número natural, é qualquer ordenação de
é um número natural, é qualquer ordenação de  elementos dentre os
elementos dentre os  elementos, em que cada maneira de tomar os elementos se diferenciam pela ordem e natureza dos elementos.
elementos, em que cada maneira de tomar os elementos se diferenciam pela ordem e natureza dos elementos.
Por exemplo, os agrupamentos de dois formados pelos elementos do conjunto A = {1, 2, 3} são: (1,2), (1,3), (2,1), (2,3), (3,1), (3,2).
Diferentes pela natureza: (1,2) e (2,3)
Pela ordem dos elementos: (1,3) e (3,1), (1,2) e (2,1)
Nesse caso, o número de arranjos é indicado por A3,2. Os arranjos podem ser calculados utilizando dois métodos, o princípio fundamental da contagem ou pela expressão:
Nesse caso, o número de arranjos é indicado por A3,2. Os arranjos podem ser calculados utilizando dois métodos, o princípio fundamental da contagem ou pela expressão:
Onde  é o total de elementos e
é o total de elementos e  o número de elementos escolhidos.
o número de elementos escolhidos.
 é o total de elementos e
é o total de elementos e  o número de elementos escolhidos.
o número de elementos escolhidos.
Exemplos de arranjos simples:
Exemplo 1:
Para ocupar os cargos de presidente e vice-presidente da Câmara Federal, candidataram-se dez deputados federais. De quantas maneiras distintas a escolha poderá ser feita?
Temos dez candidatos para ocuparem duas vagas, dessa forma, temos o seguinte arranjo A10,2.
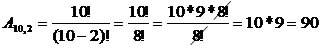
Para ocupar os cargos de presidente e vice-presidente da Câmara Federal, candidataram-se dez deputados federais. De quantas maneiras distintas a escolha poderá ser feita?
Temos dez candidatos para ocuparem duas vagas, dessa forma, temos o seguinte arranjo A10,2.
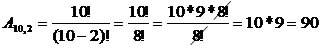
A escolha pode ser feita de 90 maneiras distintas.
Exemplo 2:
Numa corrida entre 10 competidores premia-se os dois primeiros com dois chocolates idênticos. Quais são as possibilidades de premiação?
Nesse caso, a ordem não é importante, então basta ver de quantos modos pode-se terminar a corrida. Neste caso, basta calcular:
Que é o número de maneiras de dois dos dez competidores ganhar a corrida.
Exemplo 3:
Quantas “palavras” (com sentido ou não) de 5 letras distintas podemos formar com as 20 primeiras letras do nosso alfabeto?
Não é necessário montar todas os arranjos possíveis para saber a sua quantidade, basta aplicar a fórmula:
Não é necessário montar todas os arranjos possíveis para saber a sua quantidade, basta aplicar a fórmula:
A n , p = n!
(n – p)!
Sendo que o conjunto é formado por 20 elementos (n = 20) que serão unidos de 5 em 5 (p = 5). Substitua a fórmula.
.jpg)
(n – p)!
Sendo que o conjunto é formado por 20 elementos (n = 20) que serão unidos de 5 em 5 (p = 5). Substitua a fórmula.
.jpg)
Portanto, a quantidade de arranjos formados com as 20 primeiras letras do nosso alfabeto unidas de 5 em 5 é 1860480.
Arranjos com repetição (ou completo)
O arranjo com repetição é usado quando a ordem dos elementos importa e cada elemento pode ser contado mais de uma vez.
Se em um dado conjunto um elemento é repetido a vezes, outro elemento é repetido b vezes e assim sucessivamente, o número total de permutações que podemos obter é dada por:
Exemplos de arranjos com repetição:
Exemplo 1:
Quantos anagramas podemos obter a partir das letras da palavra PARAR?
Como a palavra PARAR possui 5 letras, mas duas delas são repetidas duas vezes cada, na solução do exemplo vamos calcular P5(2, 2):
Exemplo 2:
Num determinado país, as matrículas dos automóveis são formadas por 4 letras do alfabeto (de 26 letras). Quantas matrículas distintas são possíveis arranjar desta forma?
Observemos que é possível haver matrículas como: "AAAA" ou "YYWW". Mas devemos também ter em conta que as matrículas "ABCD" e "DCBA" são diferentes, apesar de constituídas pelos mesmos elementos. Temos assim de calcular os arranjos completos  .
.
Para a primeira letra da matrícula temos 26 hipóteses; para a segunda letra,temos 26 hipóteses por cada uma das 26 primeiras; para a terceira letra, temos26 hipóteses por cada uma das 26 x 26 hipóteses anteriores; para a quarta letra, temos 26 hipóteses por cada uma das 26 x 26 x 26 hipóteses anteriores,o que perfaz o total de 26 x 26 x 26 x 26 = 264 hipóteses.
Assim, podemos concluir que . Ou, generalizando,
. Ou, generalizando,  .
.
 .
.Para a primeira letra da matrícula temos 26 hipóteses; para a segunda letra,temos 26 hipóteses por cada uma das 26 primeiras; para a terceira letra, temos26 hipóteses por cada uma das 26 x 26 hipóteses anteriores; para a quarta letra, temos 26 hipóteses por cada uma das 26 x 26 x 26 hipóteses anteriores,o que perfaz o total de 26 x 26 x 26 x 26 = 264 hipóteses.
Assim, podemos concluir que
 . Ou, generalizando,
. Ou, generalizando,  .
.
Exemplo 3:
Quatro amigos dirigem-se a uma pastelaria para comprarem, cada um, um bolo. Nessa pastelaria existem sete bolos diferentes à escolha. De quantas maneiras diferentes pode ser feita a escolha dos bolos?
Cada amigo poderá escolher entre seis bolos, por isso, aplicaremos um arranjo com repetição de sete, quatro a quatro.
7A’4 = 74 = 2401
R.: A escolha dos bolos pode ser feita de 2401 maneiras diferentes
Diferença entre arranjos simples e arranjos com repetição (completos)
Arranjos Completos (A') - Há repetição, a Ordem conta
Arranjos Simples (A) - Não há repetição, a Ordem conta
Arranjos Simples (A) - Não há repetição, a Ordem conta
Fontes: www.alunosonline.com.br
www.matematicadidatica.com.br
Questões resolvidas sobre arranjos simples e com repetição
1) Em uma urna de sorteio de prêmios existem dez bolas enumeradas de 0 a 9. Determine o número de possibilidades existentes num sorteio cujo prêmio é formado por uma sequência de 6 algarismos.
Solução:


2) Em uma empresa, quinze funcionários se candidataram para as vagas de diretor e vice-diretor financeiro. Eles serão escolhidos através do voto individual dos membros do conselho da empresa. Vamos determinar de quantas maneiras distintas essa escolha pode ser feita.
Trata-se de um agrupamento de 15 pessoas tomadas 2 a 2.
Solução:

Os cargos poderão ser ocupados de 210 maneiras distintas.
3) Em uma escola está sendo realizado um torneio de futebol de salão, no qual dez times estão participando. Quantos jogos podem ser realizados entre os times participantes em turno e returno?
Solução:
Como o campeonato possui dois turnos, os jogos Equipe A x Equipe B e Equipe B x Equipe A tratam-se de partidas distintas, então estamos trabalhando com arranjos simples onde importa a ordem dos elementos. Devemos calcular A10, 2:
4) Qual o número de anagramas que podemos formar com as letras da palavra PADRINHO?
Solução:
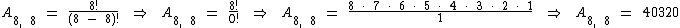
5) Em um torneio internacional de natação participaram cinco atletas europeus, dois americanos e um brasileiro.
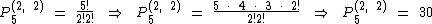
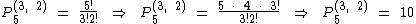
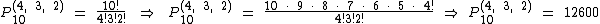
Solução:
Neste exemplo temos um arranjo simples com 8 elementos agrupados 8 a 8. Calculemos então A8, 8:
5) Em um torneio internacional de natação participaram cinco atletas europeus, dois americanos e um brasileiro.
a) De quantos modos distintos poderão ser distribuídas as medalhas de ouro, prata e bronze?
São 8 atletas (5 europeus + 2 americanos + 1 brasileiro) que vão disputar as 3 posições do pódio e é claro que importa a ordem né (ouro, prata e bronze)
A 8,3 = 8!/(8-3)! = 8!/5! = 8×7x6x5!/5! = 8×7x6 = 336
Temos 336 maneiras diferentes de preencher este pódio.
b) Em quantos resultados só aparecem atletas europeus nas três primeiras posições?
Vamos determinar em quantas destas maneiras somente os atletas europeus preenchem o pódio. São 5 atletas para 3 posições:
A 5,3 = 5!/(5-3)! = 5!/2! = 5×4x3x2!/2! = 5×4x3 = 60
Em 60 destas maneiras só aparecem atletas europeus nas primeiras posições.
c) Em quantos resultados o atleta brasileiro recebe medalha?
Agora uma destas medalhas tem que ser do brasileiro, então restam 7 atletas para disputar 2 posições:
A 7,2 = 7!/(7-2)! = 7!/5! = 7×6x5!/5! = 7×6 = 42
Mas, como importa a ordem,o atleta brasileiro pode receber a medalha de ouro, prata ou bronze, temos 3 posições diferentes para ele, daí:
42×3 = 126 resultados em que o atleta brasileiro recebe medalha.
d) Supondo que o atleta brasileiro não recebeu medalha, determine o número de resultados em que há mais atletas europeus do que americanos no pódio?
Para termos essa situação temos dois casos:
- Um dos atletas americanos recebe uma medalha no pódio (que pode ser ouro, prata ou bronze, por isso vamos x3). Então teremos 2 posições ocupadas por atletas europeus e 1 por um americano:
3 . A 5,2 . A 2,1 = 3 . 5!/3! . 2!/1! = 3.5×4.2 = 120 maneiras
- O pódio é preenchido somente por atletas europeus, logo: (fizemos já este cálculo na letra b)
A 5,3 = 5!/2! = 5×4x3 = 60 maneiras
TOTAL: 120 + 60 = 180 maneiras em que, sem que o atleta brasileiro receba medalha, há mais atletas europeus do que americanos no pódio.
6) Numa reunião de 7 pessoas há 9 cadeiras. Determine de quantos modos distintos as 7 pessoas podem sentar-se nas 9 cadeiras.
Trata-se de um problema de arranjos simples, cuja solução é encontrada calculando-se
A9,7 = 9!/(9-7)! = 9!/2! = (9.8.7.6.5.4.3.2!)/2! = 181.440
Poderíamos também resolver aplicando a regra do produto , com o seguinte raciocínio:
A primeira pessoa tinha 9 opções para sentar-se, a segunda, 8 , a terceira,7 , a quarta,6 , a quinta,5 , a sexta, 4 e finalmente a sétima, 3. Logo, o número total de possibilidades será igual a 9.8.7.6.5.4.3 = 181.440.
7) Dos números distintos que são formados com todos os algarismos do número 333669, quantos desses são ímpares?
Neste exemplo, número ímpares serão aqueles terminados em 3 ou 9.
No caso dos números terminados em 3 devemos calcular P5(2, 2), pois um dos dígitos três será utilizado na última posição e dos 5 dígitos restantes, teremos 2 ocorrências do próprio algarismo 3 e 2 ocorrências do 6:
Agora no caso dos números terminados em 9 devemos calcular P5(3, 2), pois o dígito 9 será utilizado na última posição e dos 5 dígitos que sobram, teremos 3 ocorrências do 3 e 2 ocorrências do dígito 6:
Como temos 30 números terminados em 3 e mais 10 terminados em 9, então no total temos 40 números ímpares.
Logo:
Dos números formados, 40 deles são ímpares.
8) Possuo 4 bolas amarelas, 3 bolas vermelhas, 2 bolas azuis e 1 bola verde. Pretendo colocá-las em um tubo acrílico translúcido e incolor, onde elas ficarão umas sobre as outras na vertical. De quantas maneiras distintas eu poderei formar esta coluna de bolas?
Neste caso de permutação com elementos repetidos temos um total de 10 bolas de quatro cores diferentes. Segundo a repetição das cores, devemos calcular P10(4, 3, 2):
Então:
Eu poderei formar esta coluna de bolas de 12600 maneiras diferentes.
9) Quantos números de 5 algarismos distintos
formamos com os algarismos 1,2,3,4,5,6,7,8 e 9?
10) (UFPR)
Dentre todos os números de quatro algarismos distintos formados com algarismos
pertencentes ao conjunto {3, 4, 5, 6, 7, 8, 9}, quantos são divisíveis por 2?
11) De
quantas maneiras distintas podemos classificar os 6 primeiros colocados numa
corrida de bicicleta disputada por 10 ciclistas?
12) Quantos
são os números compreendidos entre 2 000 e 3 000, compostos por algarismos
distintos escolhidos entre 1, 2, 3, 4, 5, 6, 7, 8 e 9?
13) (FUVEST 2010) Maria deve criar uma senha de 4 dígitos para sua conta bancária. Nessa senha, somente os algarismos 1,2,3,4,5 podem ser usados e um mesmo algarismo pode aparecer mais de uma vez. Contudo, supersticiosa, Maria não quer que sua senha contenha o número 13, isto é, o algarismo 1 seguido imediatamente pelo algarismo 3 . De quantas maneiras distintas Maria pode escolher sua senha?
a) 551
b) 552
c) 553
d) 554
e) 555
13) (FUVEST 2010) Maria deve criar uma senha de 4 dígitos para sua conta bancária. Nessa senha, somente os algarismos 1,2,3,4,5 podem ser usados e um mesmo algarismo pode aparecer mais de uma vez. Contudo, supersticiosa, Maria não quer que sua senha contenha o número 13, isto é, o algarismo 1 seguido imediatamente pelo algarismo 3 . De quantas maneiras distintas Maria pode escolher sua senha?
a) 551
b) 552
c) 553
d) 554
e) 555
Gabarito:
9) 15.120 10) 360 11) 151.200 12) 336 13) A
Questões sobre arranjos com elementos repetidos
1) Dos números distintos que são formados com todos os algarismos do número 333669, quantos desses são ímpares?
Neste exemplo, número ímpares serão aqueles terminados em 3 ou 9.
No caso dos números terminados em 3 devemos calcular P5(2, 2), pois um dos dígitos três será utilizado na última posição e dos 5 dígitos restantes, teremos 2 ocorrências do próprio algarismo 3 e 2 ocorrências do 6:
Agora no caso dos números terminados em 9 devemos calcular P5(3, 2), pois o dígito 9 será utilizado na última posição e dos 5 dígitos que sobram, teremos 3 ocorrências do 3 e 2 ocorrências do dígito 6:
Como temos 30 números terminados em 3 e mais 10 terminados em 9, então no total temos 40 números ímpares.
Logo:
Dos números formados, 40 deles são ímpares.
2) Possuo 4 bolas amarelas, 3 bolas vermelhas, 2 bolas azuis e 1 bola verde. Pretendo colocá-las em um tubo acrílico translúcido e incolor, onde elas ficarão umas sobre as outras na vertical. De quantas maneiras distintas eu poderei formar esta coluna de bolas?
Neste caso de permutação com elementos repetidos temos um total de 10 bolas de quatro cores diferentes. Segundo a repetição das cores, devemos calcular P10(4, 3, 2):
Então:
Eu poderei formar esta coluna de bolas de 12600 maneiras diferentes.

nao consegui resolver a 12...alguém pode explicar por favor?
ResponderExcluirO número deve ser escolhido entre 1, 2, 3, 4, 5, 6, 7, 8, 9. O número deve ter quatro algarismos (pois está entre 2000 e 3000). Para o primeiro algarismo existe apenas uma possibilidade (2), e para os outros três ainda existem 8 números disponíveis, então:
Excluir1x 8x7x6 = 336 números
Este comentário foi removido pelo autor.
ResponderExcluirEste comentário foi removido pelo autor.
ResponderExcluirA questão 1, fiquei na dúvida pois se o zero for retirado primeiro seria um número de 5 algarismos e não de 6 algarismos, e não fala se a bola que foi retirada é colocada novamente na urna?
ResponderExcluirA questão 1, fiquei na dúvida pois se o zero for retirado primeiro seria um número de 5 algarismos e não de 6 algarismos, e não fala se a bola que foi retirada é colocada novamente na urna?
ResponderExcluircorrija no arranjo com repeticao a formula esta errada, reveja sua formula, essa formula é de permutacao
ResponderExcluirAlguém pode resolver essa questão pra mim?
ResponderExcluirQtos anagramas distintos podem ser montados com as letras da palavra CASCAVEL onde as duas letras "A" apareçam juntas?
a) 2520 b)5040 c)40320 d)720 e)360
D) 720
ResponderExcluira questão sobre arranjos com elementos repetidos, são de permutacão ou arranjos? por que se for arranjo porque tem P ao invés de A...?
ResponderExcluir