Progressões geométricas (P.G)
As Progressões Geométricas são formadas por uma sequência numérica, onde estes números são definidos (exceto o primeiro) utilizando a constante q, chamada de razão. O próximo número da P.G. é o número atual multiplicado por q. Exemplo:
(1, 2, 4, 8, 16, 32, 64, 128, 256, 512, …), onde a razão é 2
A razão pode ser qualquer número racional (positivos, negativos, frações, exceto o zero). Para descobrir qual a razão de uma PG, basta escolher qualquer número da sequência, e dividir pelo número anterior.
Classificação das progressões geométricas
As PG’s podem ser classificadas em quatro tipos, de acordo com o valor da razão:
Progressão geométrica oscilante (q < 0)
Neste tipo de P.G, a razão é negativa, o que fará com que a sequência numérica seja composta de números negativos e positivos, se intercalando.
Exs: P.G (3,-6,12,-24,48,-96,192,-384,768,…), onde a razão é -2
P.G. ( -3, 6, -12, ... ), onde a razão é -2
Progressão geométrica crescente (q > 0)
Na PG crescente, a razão é sempre positiva, e por isto a sequência será formada por números crescentes, como:
P.G (1, 3, 9, 27, 81, …), onde a razão é 3
P.G ( 1, 2, 4, ... ), onde a razão é 2
Uma progressão geométrica é constante quando a sua razão é igual a 1, ou quando o primeiro termo é igual a zero. Neste caso todos os termos da P.G. têm o mesmo valor.
P.G. ( 5, 5, ..., 5 )
P.G. ( 9, 9, 9 )
No primeiro exemplo temos que a1 = 0 e nos outros dois q = 1.
As progressões geométricas decrescentes tem a razão sempre positiva e diferente de zero, e os números da sequência são sempre menores do que o número anterior:
Exs: P.G (64, 32, 16, 8, 4, 2, 1, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, ..) razão = 1/2
P.G (-1, -3, -9, -27, -81, …) onde a razão é 3 (observe que na P.G crescente temos um exemplo com a mesma razão, porém o número inicial aqui é negativo, alterando toda a sequência).
Fórmula do termo geral de um Progressão geométrica (P.G)
Numa progressão geométrica de razão q, os termos são obtidos, por definição, a partir do primeiro, da seguinte maneira:
| a1 | a2 | a3 | ... | a20 | ... | an | ... |
| a1 | a1xq | a1xq2 | ... | a1xq19 | a1xqn-1 | ... |
Assim, podemos deduzir a seguinte expressão do termo geral, também chamado enésimo termo, para qualquer progressão geométrica.
an = a1 x qn-1
|
Portanto, se por exemplo, a1 = 2 e q = 1/2, então:
an = 2 x (1/2)n-1
|
Se quisermos calcular o valor do termo para n = 5, substituindo-o na fórmula, obtemos:
a5 = 2 x (1/2)5-1 = 2 x (1/2)4 = 1/8
|
A semelhança entre as progressões aritméticas e as geométricas é aparentemente grande. Porém, encontramos a primeira diferença substancial no momento de sua definição. Enquanto as progressões aritméticas formam-se somando-se uma mesma quantidade de forma repetida, nas progressões geométricas os termos são gerados pela multiplicação, também repetida, por um mesmo número. As diferenças não param aí.
Observe que, quando uma progressão aritmética tem a razão positiva, isto é, r > 0, cada termo seu é maior que o anterior. Portanto, trata-se de uma progressão crescente. Ao contrário, se tivermos uma progressão aritmética com razão negativa, r < 0, seu comportamento será decrescente. Observe, também, a rapidez com que a progressão cresce ou diminui. Isto é conseqüência direta do valor absoluto da razão, |r|. Assim, quanto maior for r, em valor absoluto, maior será a velocidade de crescimento e vice-versa.
Em uma progressão geométrica, temos que o 1º termo equivale a 4 e a razão igual a 3. Determine o 8º termo dessa PG.
a8 = 4 * 37
a8 = 4 * 2187
a8 = 8748
O 8º termo da PG descrita é o número 8748.
Exemplo 2
Dada a PG (3, 9, 27, 81, ...), determine o 20º termo.
a20 = 3 * 319
a20 = 3 * 1.162.261.467
a20 = 3.486.784.401
Exemplo 3:
Sabe-se que o quarto termo de uma PG crescente é igual a 20 e o oitavo termo é igual a 320. Qual a razão desta PG?
Temos a4 = 20 e a8 = 320. Logo, podemos escrever: a8 = a4 . q8-4 . Daí, vem: 320 = 20.q4
Então q4 =16 e portanto q = 2.
Temos a4 = 20 e a8 = 320. Logo, podemos escrever: a8 = a4 . q8-4 . Daí, vem: 320 = 20.q4
Então q4 =16 e portanto q = 2.
Nota: Uma PG genérica de 3 termos, pode ser expressa como:
(x/q, x, xq), onde q é a razão da PG.
(x/q, x, xq), onde q é a razão da PG.
Principais propriedades das Progressões geométricas (P.Gs)
Propriedade 1 - em toda P.G, um termo é a média geométrica dos termos imediatamente anterior e posterior.
Exemplo: PG (A,B,C,D,E,F,G)
Temos então: B2 = A . C ; C2 = B . D ; D2 = C . E ; E2 = D . F etc.
Exemplo: PG (A,B,C,D,E,F,G)
Temos então: B2 = A . C ; C2 = B . D ; D2 = C . E ; E2 = D . F etc.
Exemplo:
Na P.G (3, 6, 12), temos:
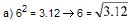
Propriedade 2 - o produto dos termos equidistantes dos extremos de uma PG é constante.
Exemplo: P.G ( A,B,C,D,E,F,G)
Temos então: A . G = B . F = C . E = D . D = D2
Temos então: A . G = B . F = C . E = D . D = D2
Na P.G. (4, 8, 16, 32, 64), temos:
4.64 = 8.32 = 256
propriedade 3
A seqüência (a, b, c), com a 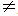 0, se, e somente se, o quadrado do termo médio é igual ao produto dos extremos, isto é, b2 = 4ac.
0, se, e somente se, o quadrado do termo médio é igual ao produto dos extremos, isto é, b2 = 4ac.
Exemplo: P.G (1, 2, 4, 8, 16)
4² = 4.1.4
4 = 4
INTERPOLAÇÃO GEOMÉTRICA
Interpolar, Inserir ou Intercalar m meios geométricos entre dois números reais a e b significa obter uma P.G. de extremos a e b, com m+2 elementos. Para realização da interpolação de meios geométricos precisamos utilizar a fórmula do termo geral da PG:

Para interpolar meios geométricos, também é necessário conhecer o valor da razão da PG.
Para interpolar meios geométricos, também é necessário conhecer o valor da razão da PG.
Exemplo 1: Uma P.G é formada por 6 termos, onde a1 = 4 e a6 = 972. Determine os meios geométricos existentes entre a1 e a6.
Solução: Para interpolar os meios geométricos entre 4 e 972 precisamos determinar o valor da razão da P.G. Para isso, vamos utilizar a fórmula do termo geral.

Sabemos que a razão da PG é 3 e que cada termo, a partir do segundo, é obtido fazendo o produto entre o termo anterior e a razão. Assim, teremos:
Solução: Para interpolar os meios geométricos entre 4 e 972 precisamos determinar o valor da razão da P.G. Para isso, vamos utilizar a fórmula do termo geral.

Sabemos que a razão da PG é 3 e que cada termo, a partir do segundo, é obtido fazendo o produto entre o termo anterior e a razão. Assim, teremos:

Exemplo 2: Determine os termos que faltam na sequência numérica (3, _, _, _, _, _, _, _, _, 1536) para que tenhamos uma progressão geométrica.
Solução: Observe que descobrir os termos que faltam na sequência com extremos 3 e 1536 significa interpolar meios geométricos. Dessa forma, precisamos determinar o valor da razão dessa PG.
Pela sequência numérica dada, sabemos que a1 = 3 e a10 = 1536 (pois 1536 ocupa a décima posição na sequência). Utilizando a fórmula do termo geral, teremos:

Conhecido o valor da razão, podemos determinar os termos que faltam na sequência:

Solução: Observe que descobrir os termos que faltam na sequência com extremos 3 e 1536 significa interpolar meios geométricos. Dessa forma, precisamos determinar o valor da razão dessa PG.
Pela sequência numérica dada, sabemos que a1 = 3 e a10 = 1536 (pois 1536 ocupa a décima posição na sequência). Utilizando a fórmula do termo geral, teremos:

Conhecido o valor da razão, podemos determinar os termos que faltam na sequência:

Exemplo 3: Distribua 4 números entre 800 e 25 para que a sequência numérica formada seja uma progressão geométrica.
Solução: Queremos interpolar 4 meios geométricos entre 800 e 25.
(800, _, _, _, _, 25)
Precisamos conhecer o valor da razão dessa PG. Para isso, utilizaremos a fórmula do termo geral.
Sabemos que: n = 6, a1 = 800 e a6 = 25. Segue que:
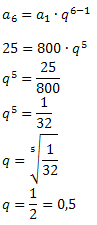
Conhecido o valor da razão, podemos determinar os termos que devem ficar compreendidos entre 800 e 25.
a2 = a1*q = 800*0,5 = 400
a3 = a2*q = 400*0,5 = 200
a4 = a3*q = 200*0,5 = 100
a5 = a4*q = 100*0,5 = 50
Portanto, interpolando 4 meios geométricos entre 800 e 25, obtemos a seguinte PG:
(800, 400, 200, 100, 50, 25)
a2 = a1*q = 800*0,5 = 400
a3 = a2*q = 400*0,5 = 200
a4 = a3*q = 200*0,5 = 100
a5 = a4*q = 100*0,5 = 50
Portanto, interpolando 4 meios geométricos entre 800 e 25, obtemos a seguinte PG:
(800, 400, 200, 100, 50, 25)
Soma dos n primeiros termos de uma P.G
Seja a PG (a1, a2, a3, a4, ... , an , ...) . Para o cálculo da soma dos n primeiros termos Sn, vamos considerar o que segue:
Sn = a1 + a2 + a3 + a4 + ... + an-1 + an
Sn = a1 + a2 + a3 + a4 + ... + an-1 + an
Multiplicando ambos os membros pela razão q vem:
Sn.q = a1 . q + a2 .q + .... + an-1 . q + an .q
Sn.q = a1 . q + a2 .q + .... + an-1 . q + an .q
Conforme a definição de PG, podemos reescrever a expressão como:
Sn . q = a2 + a3 + ... + an + an . q
Sn . q = a2 + a3 + ... + an + an . q
Observe que a2 + a3 + ... + an é igual a Sn - a1 . Logo, substituindo, vem:
Sn . q = Sn - a1 + an . q
Sn . q = Sn - a1 + an . q
Daí, simplificando convenientemente, chegaremos à seguinte fórmula da soma:
Se substituirmos an = a1 . qn-1 , obteremos uma nova apresentação para a fórmula da soma, ou seja:
Exemplo:
Calcule a soma dos 10 primeiros termos da PG (1,2,4,8,...)
Temos:
Temos:
Observe que neste caso a1 = 1.
Soma dos termos de uma PG decrescente e ilimitada (infinita)
Considere uma P.G ILIMITADA ( infinitos termos) e decrescente. Nestas condições, podemos considerar que no limite teremos an = 0. Substituindo na fórmula anterior, encontraremos:
Exemplo 1: Considerando os dados do exemplo 2, determine a soma dos 20 primeiros elementos dessa PG.

Exemplo 2:
Dada a PG (1,1/2,1/4,1/8,1/16…), obtenha a soma de todos os seus termos.
Solução:
Solução:
Temos que:
a1 = 1
a1 = 1
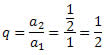
Segue que:
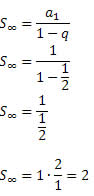
Exemplo 3:
Resolva a equação: x + x/2 + x/4 + x/8 + x/16 + ... =100
O primeiro membro é uma PG de primeiro termo x e razão 1/2. Logo, substituindo na fórmula, vem:
Dessa equação encontramos como resposta x = 50.
Produto dos termos de uma Progressão geométrica
Como feito no caso da soma, vamos agora deduzir a fórmula de cálculo do produto dos termos de uma progressão geométrica. Vejamos:
Portanto a fórmula para o cálculo do produto dos termos de uma P.G. finita, ou do produto dos n primeiros termos de uma P.G. é:
Questões resolvidas sobre Progressões Geométricas (P.G)
1) Qual é a soma dos termos da P.G. ( 8, 56, 392, ..., 134456)?
Solução:
A partir do enunciado podemos calcular a razão da progressão:
Para calcularmos a soma dos termos, primeiramente precisamos saber quantos eles são. Os dados disponíveis que temos para calcular esta quantidade são:
Calculando n temos:
Agora que sabemos quantos termos são, podemos calcular a soma dos mesmos:
Logo:
A soma dos termos da referida P.G. é igual a 156864
2) Ao somarmos o segundo, o quinto e o sexto termo de uma P.G. obtemos 400. Ao somarmos o terceiro, o sexto e o sétimo termo, obtemos o dobro disto. Quanto obteremos se somarmos os três primeiros termos desta progressão?
Solução:
Solução:
A partir do enunciado montamos duas equações:
Podemos escrevê-las em função do primeiro termo para ficarmos com apenas duas variáveis, a1 e q:
Repare que podemos colocar q em evidência na segunda equação:
Perceba que esta providência nos permitirá encontrar o valor de q, já que o valor que está entre parênteses é exatamente igual à primeira equação:
Substituindo q pelo seu valor na primeira equação, já com os termos colocados em função de a1, encontraremos o valor deste termo:
Finalmente, sabendo que a1 = 8 e que q = 2, podemos calcular o valor da soma dos três primeiro termos:
Portanto:
A soma dos três primeiros termos desta progressão é igual a 56.
3) ) Qual é o valor de x na P.G.(x - 40, x, x + 200)?
Solução:
Solução:
Como x é média geométrica entre x - 40 e x + 200 temos:
Portanto:
O valor de x na progressão geométrica é 50.
4) O produto dos 7 termos de uma P.G. é igual a 4586471424. Qual é o quarto termo?
Solução:
Se representarmos todos os termos desta progressão em função de a4 teremos:
P.G. ( a4q-3, a4q-2, a4q-1, a4, a4q, a4q2, a4q3 ).
A representação do produto dos termos será então:
Perceba que na expressão acima q-3 anula q3, assim como q-2 anula q2 e q-1 anula q, deixando a mesma apenas com a variável a4. Isto ocorre apenas porque utilizamos o termo central como referência. Se tivéssemos escolhido qualquer outro termo, como o a3, por exemplo, para representarmos todos os outros termos em função dele, isto não iria ocorrer pois ele não é o termo central. Em função disto é fácil concluir que se a progressão tivesse um número par de termos, tal técnica não poderia ser utilizada.
Após esta breve explicação vamos continuar a resolução do exercício:
Portanto:
O quarto termo é igual a 24.
5) (Vunesp – SP – Adaptado)Várias tábuas iguais estão em uma madeireira. Elas deverão ser empilhadas respeitando a seguinte ordem: uma tábua na primeira vez e, em cada uma das vezes seguintes, tantas quantas já estejam na pilha. Por exemplo:

Determine a quantidade de tábuas empilhadas na 12ª pilha.
Solução:
As tábuas são empilhadas de acordo com uma progressão geométrica de razão 2. Então:
an = a1 * q n–1
a12 = 1 * 2 12–1
a12 = 1 * 2 11
a12 = 1 * 2048
a12 = 2048
Na 12ª pilha teremos 2048 tábuas.
6) Qual o primeiro termo de uma PG com 8 termos, onde o último vale -1 e a razão 1/2 ?
an = a1 * q n–1
a12 = 1 * 2 12–1
a12 = 1 * 2 11
a12 = 1 * 2048
a12 = 2048
Na 12ª pilha teremos 2048 tábuas.
6) Qual o primeiro termo de uma PG com 8 termos, onde o último vale -1 e a razão 1/2 ?
Solução:
a1 = ? ; an = -1 ; n = 8; q = 1/2;an = a1 . qn – 1-1 = a1 . 1/28 – 1
=>
-1 = a1 . 1/27
=>
-1 = a1. 1/128
=>
a1 = -128
O primeiro termo dessa P.G. vale -128, e como podemos observar trata-se de uma P.G. do tipo decrescente.
a) 10
b) 12
c) 14
d) 16
e) 18
b) 12
c) 14
d) 16
e) 18
Solução:
Sejam (a1, a2, a3, …) a PA de razão r e (g1, g2, g3, …) a PG de razão q. Temos como condições iniciais:
(1) a1 = g1 = 4
(2) a3 > 0, g3 > 0 e a3 = g3
(3) a2 = g2 + 2
Reescrevendo (2) e (3) utilizando as fórmulas gerais dos termos de uma PA e de uma PG e (1) obtemos o seguinte sistema de equações:
(4) a3 = a1 + 2r e g3 = g1.q2 => 4 + 2r = 4q2
(5) a2 = a1 + r e g2 = g1.q => 4 + r = 4q + 2
Expressando, a partir da equação (5), o valor de r em função de q e substituindo r em (4) vem:
(5) => r = 4q + 2 – 4 => r = 4q – 2
(4) => 4 + 2(4q – 2) = 4q2 => 4 + 8q – 4 = 4q2 => 4q2 – 8q = 0
=> q(4q – 8) = 0 => q = 0 ou 4q – 8 = 0 => q = 2
Como g3 > 0, q não pode ser zero e então q = 2. Para obter r basta substituir q na equação (5):
r = 4q – 2 => r = 8 – 2 = 6
Para concluir calculamos a3 e g3:
a3 = a1 + 2r => a3 = 4 + 12 = 16
g3 = g1.q2 => g3 = 4.4 = 16
8) (UFSCAR/2000) A condição para que três números a, b e c estejam, simultaneamente, em progressão aritmética e em progressão geométrica é que:
a) ac = b2
b) a + c = 2
c) a + c = b2
d) a = b = c
e) ac = 2b
Solução:
A condição para que a, b e c sejam ao mesmo tempo uma PA de razão r e uma P.G de razão q é:
(1) b = a + r = aq => r = a(q – 1)
(2) c = b + r = bq => r = b(q – 1)
De (1) e (2) vem:
a(q – 1) = b(q – 1) => (a – b)(q – 1) = 0
Para que o produto seja igual a zero:
ou a – b = 0 ou q – 1 = 0 ou ambas => ou a = b ou q = 1 ou ambas
Como se trata de uma PG se a é igual a b, necessariamente q = 1. A recíproca também é verdadeira, isto é, se q = 1 então a = b. Logo a = b e q = 1. Daqui, de (1) e de (2) segue que r = 0 e b = c = a.
9) (UFSC) Numa P.G de 6 termos, a razão é 5. O produto do 1º termo com o último é 12500. Determine o valor do 3º termo.
(Obs: Considere a P.G de termos positivos)
Solução:
A1.A6 = 12500
A1 = 12500
A6
An = A1 . qn-1
A6 = 12500 . 56-1
A6
A6.A6 = 12500.3125
(A6)2 = 39062500
A6 = 6250
An = A1 . qn-1
A3 = A1 . 53 – 1
A3 = 12500 . 52
6250
A3 = 2.25
A3 = 50
10) Sabendo que a sequência a seguir é uma progressão geométrica decrescente, encontre o que se pede:
( -1, x , 4x+3 , ... , -243 )
a) a razão da P.G
b) o número de termos da P.G
c) a soma de todos os termos da P.G.
Solução:
a) (-1).(4x + 3) = x2
-4x – 3 = x2
x2+4x+3 = 0
Por soma e produto:
Soma = + = -4
Produto = . = 3
As raízes serão -3 ou -1, primeiro substituímos x por -3 na sequência, em seguida por -1:
( -1, x , 4x+3 , ... , -243 )
( -1, -3 , 4(-3)+3 , ... , -243 )
( -1, -3 , -9 , ... , -243 )
Ou
( -1, x , 4x+3 , ... , -243 )
( -1, -1 , 4(-1)+3 , ... , -243 )
( -1, -1 , -1 , ... , -243 )
Percebemos que a segunda progressão é falsa, pois é constante, sempre -1, e assim não pode ser -243 seu último termo, além disso, a questão afirma que a progressão é decrescente, então, tomamos a sequência 1 como referência:
( -1, -3 , -9 , ... , -243 )
A razão será:
q = A2
A1
q = -3
-1
q = 3
b) An = A1 . qn-1
-243 = -1.3n-1
Como a variável está no expoente, temos uma equação exponencial, devemos igualar as bases:
-243 = -1.3n-1
3n-1 = 243
3n-1 = 35
Se as bases estão iguais, igualamos os expoentes:
n-1 = 5
n = 5+1
n = 6
A progressão possui 6 termos.
c) Se a progressão possui 6 termos, podemos obtê-los e somar todos, se a razão é 3, basta multiplicar por esse valor e ter o termo seguinte:
( -1, -3 , -9 , -9.3, -9.3.3, -243 )
( -1, -3 , -9 , -27, -81, -243 )
A soma de todos:
Sn = -1 + (-3) + (-9) + (-81) + (-243)
Sn = -364
11) Um carro, cujo preço à vista é R$ 24 000,00, pode ser adquirido dando-se uma entrada e o restante em 5 parcelas que se encontram em progressão geométrica. Um cliente que optou por esse plano, ao pagar a entrada, foi informado que a segunda parcela seria de R$ 4 000,00 e a quarta parcela de R$ 1 000,00. Quanto esse cliente pagou de entrada na aquisição desse carro?
Solução:
an = a1 * q n–1
a2 = 4000
a4 = 1000
a4 = 1000
a2 = a1 * q
4000 = a1 * q
a1 = 4000 / q
4000 = a1 * q
a1 = 4000 / q
a4 = a1 * q3
1000 = 4000 / q * q3
1000 / 4000 = q3 / q
1 / 4 = q2
√1/4 = √q2
q = 1/2
1000 = 4000 / q * q3
1000 / 4000 = q3 / q
1 / 4 = q2
√1/4 = √q2
q = 1/2
a1 = 4000 / 1/2
a1 = 4000 * 2
a1 = 8000
a1 = 4000 * 2
a1 = 8000
1ª prestação: R$ 8 000,00
2ª prestação: R$ 4 000,00
3ª prestação: R$ 2 000,00
4ª prestação: R$ 1 000,00
5ª prestação: R$ 500,00
Soma total das prestações: R$ 15 500,00
Entrada (valor do carro menos o total das prestações)
R$ 24 000,00 – R$ 15 500,00 = R$ 8 500,00
O valor da entrada foi de R$ 8 500,00
Exercícios sobre Progressão Geométrica
Exercícios sobre Progressão Geométrica
1) (PUC-SP) O terceiro termo de uma sequência geométrica é 10 e o sexto termo é 80. Então, a razão é:
a) 1
b) -1
c) -2
d) 2
e) 3
2) (CESGRANRIO/2012) Seja a progressão geométrica:  O quarto termo dessa progressão é:
O quarto termo dessa progressão é:
 O quarto termo dessa progressão é:
O quarto termo dessa progressão é:
a) 0
b) 

c) 

d) 1
e) 5
3) Uma sequência de números k1 , k2 , k3 , k4 ,....,kn é denominada Progressão Geométrica - PG - de n termos quando, a partir do segundo termo, cada termo dividido pelo imediatamente anterior for igual a uma constante r denominada razão. Sabe-se que, adicionando uma constante x a cada um dos termos da sequência (p - 2); p; e (p + 3) ter-se-á uma PG. Desse modo, o valor de x, da razão e da soma dos termos da PG são, respectivamente, iguais a
a) (6 - p); 2/3; 21.
b) (p +6); 3/2; 19.
c) 6; (6 – p); 21.
d) (6 - p); 3/2; 19.
e) (p - 6); p; 20.
4) Qual é a soma dos termos da sequência (x - 2, 3x - 10, 10 + x, 5x + 2), para que a mesma seja uma progressão geométrica crescente?
a) 52
b) 60
c) 40
d) 48
e) 64
5) (CEPRJ) Em uma progressão geométrica, o segundo termo é 27–2 , o terceiro termo é 94 , e o quarto termo é 3n . O valor de n é:
a) 22
b) 20
c) 18
d) 16
e) 24
6) (PUC-RIO 2008) Na seqüência 1, 3, 7,…, cada termo é duas vezes o anterior mais um. Assim, por exemplo, o quarto termo é igual a 15. Então o décimo termo é:
a) 1000
b) 1002
c) 1015
d) 1023
e) 1024
7) (UDESC 2009) Se os números reais x, y e z formarem, nesta ordem, uma progressão geométrica de razão 10x , pode-se afirmar que log(xyz) é igual a:
| a) | |
| b | |
| c) | |
| d) | |
| e) |
8) (CEFET-MG) Quatro números x; -6; 3x + 3 e y formam, nessa ordem, uma P.G. Então, a diferença em módulo, entre os dois possíveis valores de y é igual a :
a) 21/2 b) 19/2 c) 17/2 d) 21 e) 19
9) Determine os três valores de um P.G tal que o seu produto seja 3375 e a soma do 1º termo com o 3º termo seja igual a 78.
10) Subtraindo-se um mesmo número de 6, 14 e 38, obtemos nessa ordem, uma P.G. Qual é razão dessa P.G.
a) 9 b) 6 c) 5 d) 4 e) 3
11) Um pêndulo, oscilando, percorre sucessivamente 18 cm, 15 cm, 12 cm, ... . A soma dos percursos até parar é:
a) 45 cm b) 63 cm c) 90 cm d) 126 cm e) 140 cm
12) (PUC) Se a razão de uma P. G. é maior que 1 e o primeiro termo é negativo, a P. G. é chamada:
a) decrescente
b) crescente
c) constante
d) alternante
e) singular
13) (FIA) Numa progressão geométrica, tem-se a3 = 40 e a6 = -320. A soma dos oito primeiros termos é:
a) -1700
b) -850
c) 850
d) 1700
e) 750

Gabarito:
1) D 2) D 3) D 4) B 5) A 6) D 7) C 8) A 9) 3, 15 e 75 10) E 11) B 12) A
13) B 14) x = 1/3 15) (2, 6, 18, 54, 162, 486, ...)
a) 21/2 b) 19/2 c) 17/2 d) 21 e) 19
9) Determine os três valores de um P.G tal que o seu produto seja 3375 e a soma do 1º termo com o 3º termo seja igual a 78.
10) Subtraindo-se um mesmo número de 6, 14 e 38, obtemos nessa ordem, uma P.G. Qual é razão dessa P.G.
a) 9 b) 6 c) 5 d) 4 e) 3
11) Um pêndulo, oscilando, percorre sucessivamente 18 cm, 15 cm, 12 cm, ... . A soma dos percursos até parar é:
a) 45 cm b) 63 cm c) 90 cm d) 126 cm e) 140 cm
12) (PUC) Se a razão de uma P. G. é maior que 1 e o primeiro termo é negativo, a P. G. é chamada:
a) decrescente
b) crescente
c) constante
d) alternante
e) singular
13) (FIA) Numa progressão geométrica, tem-se a3 = 40 e a6 = -320. A soma dos oito primeiros termos é:
a) -1700
b) -850
c) 850
d) 1700
e) 750
14) (Concurso da Polícia Rodoviária Federal)

15) Insira 4 meios geométricos entre 2 e 486, nesta ordem.
Gabarito:
1) D 2) D 3) D 4) B 5) A 6) D 7) C 8) A 9) 3, 15 e 75 10) E 11) B 12) A
13) B 14) x = 1/3 15) (2, 6, 18, 54, 162, 486, ...)
Fontes: http://www.brasilescola.com/matematica/progressao-geometrica.htm
eu gostei muito mesmo nota mil
ResponderExcluirÓtimo gostei muito
ResponderExcluir