Princípio Fundamental da Contagem e Fatorial - teoria e questões

Artigo sobre o princípio fundamental da contagem e fatorial com exercícios resolvidos e propostos.

Princípio Fundamental da Contagem

Para entendermos o princípio fundamental da contagem vamos analisar a seguinte situação: João possui 4 camisas, 3 calças, 2 pares de meia e 2 pares de sapatos. De quantas maneiras diferentes ele pode se vestir?

Observe os esquemas a seguir:

Cada esquema representa todas as possíveis combinações envolvendo os objetos do vestuário de João. Uma maneira mais simplificada e eficaz de resolver tal situação consiste em determinar a multiplicação entre a quantidade de elementos de cada conjunto. Observe:

4 * 3 * 2 * 2 = 48 combinações. 

De acordo com o princípio fundamental da contagem, se um evento é composto por duas ou mais etapas sucessivas e independentes, o número de combinações será determinado pelo produto entre as possibilidades de cada conjunto.

Observe outro exemplo:

Numa lanchonete há 8 tipos de sanduíche, 5 tipos de sucos e 6 tipos de sorvetes. Quantas são as possíveis combinações de um lanche nessa lanchonete?

Utilizando o princípio fundamental da contagem temos:

8 * 5 * 6 = 240 maneiras de realizar um lanche. 

Fatorial

O fatorial de um número n (n pertence ao conjunto dos números naturais) é sempre o produto de todos os seus antecessores, incluindo si próprio e excluindo o zero. A representação é feita pelo número fatorial seguido do sinal de exclamação, n! . Exemplo:

1! = 1 
2! = 2 * 1 = 2 
3! = 3 * 2 *1 = 6 
4! = 4 * 3 * 2 * 1 = 24 
5! = 5 * 4 * 3 * 2 * 1 = 120 
6! = 6 * 5 *4 * 3 * 2 * 1 = 720 
7! = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5 040 
8! = 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 40 320 
9! = 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 362 880 
10! = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 3 628 800 

Importante: n >= 0 (n maior ou igual a zero) , ou seja, não existe fatorial para números negativos.

* O fatorial de 0 ( 0! ) é 1, pois o produto de número nenhum é 1.

O numero fatorial pode ser modificado para outras formas:

n! = n . (n-1) . (n-2) . (n-3)!

Exemplo:

6! = 6 . (6-1) . (6-2) . (6-3)!

6! = 6 . 5 . 4 . 3!

6! = 120 . 3!

6! = 120 . 3 . (3-1) . (3-2)!

6! = 120 . 3 . 2 . 1!

6! = 120 . 6 = 720

Exemplo 2

Vamos calcular o valor de 12! / 8! . Nesse caso, se desenvolvermos os fatoriais dos números e depois efetuarmos a divisão, o método de resolução estará correto. Mas essa forma de resolução pode se tornar complexa para números elevados, por isso devemos desenvolver o fatorial do maior número até chegarmos ao fatorial do menor número, simplificando os fatoriais semelhantes. Observe:

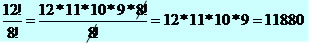
Exemplo 3

Outra forma de resolução de fatoriais é quando ocorre a soma de fatoriais. Nesse caso podemos utilizar a fatoração por evidência. Observe:

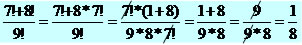
Exemplo 4

Outras situações exigem técnicas de desenvolvimento dos fatoriais para que simplificações sejam efetuadas. Veja:

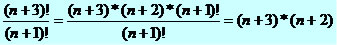
n² + 2n + 3n + 6
n² + 5n +6

Fontes: http://www.mundoeducacao.com.br/
            http://matematicasemduvida.blogspot.com.br/
           http://ensinodematemtica.blogspot.com.br/

Questões de vestibular sobre princípio fundamental da contagem e fatorial

1) (UNIFOR) - A soma de todos os números primos que são divisores de 30! é :

a) 140

b) 139

c) 132

d) 130

e) 129

Solução:

Seja S = 30!, então 

S = 30.29.28...3.2.1

Sabemos que como S é obtido pelo produto dos números naturais de 1 a 30,

logo todos os números primos que aparecem nesse intervalo são divisores de S = 30!.

portanto a soma  é igual a 

2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29 = 129

opção "e"

2)  Resolver a equação (n + 2)! + (n + 1)! = 15 . n!

Solução:

(n + 2)! + (n + 1)! = 15 . n!

(n + 2) . (n + 1) . n! + (n + 1) . n! = 15 . n!

Colocando  (n + 1) . n! em evidência:

(n + 1) . n! [(n + 2) + 1] = 15 . n!

(n + 1) . n! . (n + 3) = 15 . n! 

Dividindo os dois membros por n! (podemos, pois n! ≠ 0)

(n + 1) . (n + 3) = 15 ► n² + 4n - 12 = 0

Resolvendo a equação, encontramos n = - 6 ou n = 2.
Como n = -6 não convém, pois devemos ter n € N, a resposta é apenas n = 2

Logo, S = {2}

3) (UFJF–MG) Newton possui 9 livros distintos, sendo 4 de Geometria, 2 de Álgebra e 3 de Análise. O número de maneiras pelas quais Newton pode arrumar esses livros em uma estante, de forma que os livros de mesmo assunto permaneçam juntos, é:

a) 288
b) 296
c) 864
d) 1728
e) 2130

Solução:

4 livros de Geometria = P4                                      
2 livros de Álgebra = P2
3 livros de Análise = P3

P4 * P2 * P3 * P3 = 4! * 2! * 3!

4! = 4 * 3 * 2 * 1 = 24
2! = 2
3! = 3 * 2 * 1 = 6

P4 * P2 * P3 * P3 = 24 * 2 * 6 * 6
P4 * P2 * P3 * P3 = 1728 maneiras

Resposta correta item d.

4) Um casal e seus quatro filhos vão ser colocados lado a lado para tirar uma foto. Se todos os filhos devem ficar entre os pais, de quantos modos distintos os seis podem posar para tirar a foto?

a) 24
b) 48
c) 96
d) 120
e) 720

Solução:

Os pais deverão ocupar os extremos:
P ____ ____  ____ ____ M  ou M ____ ____ ____ ____ P
2 * P4 = 2 * 4! = 2 * 4 * 3 * 2 * 1 = 48 maneiras
Resposta correta item b.

5) (ITA–SP) Quantos números de seis algarismos distintos podemos formar usando os dígitos 1, 2, 3, 4, 5 e 6, nos quais o 1 e o 2 nunca ocupam posições adjacentes (juntos), mas o 3 e o 4 sempre ocupam posições adjacentes? 

a) 144
b) 180
c) 240
d) 288
e) 360

Solução:

3 e o 4 ocupando posições adjacentes
5! * 2! = 120 * 2 = 240 números

1 e o 2 juntos e o 3 e o 4 juntos
4! * 2! * 2! = 24 * 2 * 2 = 96 números

3 e o 4 juntos e o 1 e o 2 nunca juntos
240 – 96 = 144 números

Resposta correta item a.

6) Simplifique a expressão:                                       

Solução: 

7) Resolva as seguintes equações fatoriais:

Solução: 

8) se (n + 1)! = 10 n!, então ( n - 1 )² vale :

a) 100

b) 81

c) 64

d) 36

e) 25

Solução :

(n+1)! = 10 n!

(n+1) . n! = 10 n! , dividimos tudo por n! , então

n + 1 = 10

n = 10 - 1

n = 9

portanto, (n - 1)² = (9 - 1)²

               (n - 1)² = 8²

               (n - 1)² = 64

opção "c"

10) (Unitau – SP – Adaptada) Sendo n ≠ 0, assinale a alternativa que possui o(s) valor(es) que satisfaz(em) a equação abaixo:

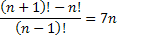
a.  7                            b.  0 e 7                            c.  0 e 10
d.  1                            e.  0 e 2                                             

Solução:

Note que no numerador temos dois termos, portando, dividiremos essa fração em duas para facilitar a simplificação dos fatoriais.

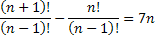
Devemos obter no numerador um número fatorial que simplifique com (n-1)!. Portanto:

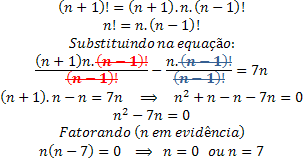
Determinamos dois valores para a incógnita do fatorial, contudo a condição inicial do problema é: n ≠ 0. Portanto, a única solução que podemos utilizar é n=7.

11) (UFRN) Se (x+1)! = 3(x!), então x é igual a:

a) 1
b) 2
c) 3
d) 4
e) 5

12) (PUC-SP) Se (n-6)! = 720, então n é igual á:

a) 12
b) 576
c) 16
d) 4
e) 30

13)  Resolva as equações fatoriais abaixo:

a) (n+1)! / (n-1)!=12

b) n! / (n-2)! = 20

c) (n-1)! (n+2)! / n! (n+1)! = 12

14) (FGV-SP) simplifique a expressão 5M!-2(M+1)!/M!

15) (UECE) O valor de 12!-(12+1)!/12! é : 

a) 4              b) 3                 c) 2              d) 1                e) 0

Gabarito:

11) B   12) A   13) a) n²+n-12=0    b) n²-n-20=0      c) n = 2/11   14) 5M-2/M     15) D