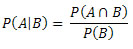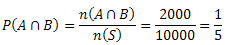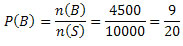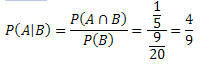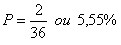Introdução à Probabilidade
Chama-se experimento aleatório àquele cujo resultado é imprevisível, porém pertence necessariamente a um conjunto de resultados possíveis denominado espaço amostral.
Qualquer subconjunto desse espaço amostral é denominado evento.
Se este subconjunto possuir apenas um elemento, o denominamos evento elementar.
Por exemplo, no lançamento de um dado, o nosso espaço amostral seria U = {1, 2, 3, 4, 5, 6}.
Exemplos de eventos no espaço amostral U:
A: sair número maior do que 4: A = {5, 6}
B: sair um número primo e par: B = {2}
C: sair um número ímpar: C = {1, 3, 5}
Nota: O espaço amostral é também denominado espaço de prova.
Trataremos aqui dos espaços amostrais equiprováveis, ou seja, aqueles onde os eventos elementares possuem a mesma chance de ocorrerem.
Por exemplo, no lançamento do dado acima, supõe-se que sendo o dado perfeito, as chances de sair qualquer número de 1 a 6 são iguais. Temos então um espaço equiprovável.
Em oposição aos fenômenos aleatórios, existem os fenômenos determinísticos, que são aqueles cujos resultados são previsíveis, ou seja, temos certeza dos resultados a serem obtidos.
Normalmente existem diversas possibilidades possíveis de ocorrência de um fenômeno aleatório, sendo a medida numérica da ocorrência de cada uma dessas possibilidades, denominada Probabilidade.
Consideremos uma urna que contenha 49 bolas azuis e 1 bola branca. Para uma retirada, teremos duas possibilidades: bola azul ou bola branca. Percebemos entretanto que será muito mais frequente obtermos numa retirada, uma bola azul, resultando daí, podermos afirmar que o evento "sair bola azul" tem maior probabilidade de ocorrer, do que o evento "sair bola branca".
2 – Conceito elementar de Probabilidade
Seja U um espaço amostral finito e equiprovável e A um determinado evento ou seja, um subconjunto de U. A probabilidade p(A) de ocorrência do evento A será calculada pela fórmula
p(A) = n(A) / n(U)
onde:
n(A) = número de elementos de A e n(U) = número de elementos do espaço de prova U.
Vamos utilizar a fórmula simples acima, para resolver os seguintes exercícios introdutórios:
Considere o lançamento de um dado. Calcule a probabilidade de:
a) sair o número 3:
Temos U = {1, 2, 3, 4, 5, 6} [n(U) = 6] e A = {3} [n(A) = 1]. Portanto, a probabilidade procurada será igual a p(A) = 1/6.
b) sair um número par: agora o evento é A = {2, 4, 6} com 3 elementos; logo a probabilidade procurada será p(A) = 3/6 = 1/2.
c) sair um múltiplo de 3: agora o evento A = {3, 6} com 2 elementos; logo a probabilidade procurada será p(A) = 2/6 = 1/3.
d) sair um número menor do que 3: agora, o evento A = {1, 2} com dois elementos. Portanto,p(A) = 2/6 = 1/3.
e) sair um quadrado perfeito: agora o evento A = {1,4} com dois elementos. Portanto, p(A) = 2/6 = 1/3.
Considere o lançamento de dois dados. Calcule a probabilidade de:
a) sair a soma 8
Observe que neste caso, o espaço amostral U é constituído pelos pares ordenados (i,j), onde i = número no dado 1 e j = número no dado 2.
É evidente que teremos 36 pares ordenados possíveis do tipo (i, j) onde i = 1, 2, 3, 4, 5, ou 6, o mesmo ocorrendo com j.
As somas iguais a 8, ocorrerão nos casos:(2,6),(3,5),(4,4),(5,3) e (6,2). Portanto, o evento "soma igual a 8" possui 5 elementos. Logo, a probabilidade procurada será igual a p(A) = 5/36.
b) sair a soma 12
Neste caso, a única possibilidade é o par (6,6). Portanto, a probabilidade procurada será igual a p(A) = 1/36.
Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule as probabilidades seguintes:
a) sair bola azul
p(A) = 6/20 = 3/10 = 0,30 = 30%
b) sair bola vermelha
p(A) = 10/20 =1/2 = 0,50 = 50%
c) sair bola amarela
p(A) = 4/20 = 1/5 = 0,20 = 20%
Vemos no exemplo acima, que as probabilidades podem ser expressas como porcentagem. Esta forma é conveniente, pois permite a estimativa do número de ocorrências para um número elevado de experimentos. Por exemplo, se o experimento acima for repetido diversas vezes, podemos afirmar que em aproximadamente 30% dos casos, sairá bola azul, 50% dos casos sairá bola vermelha e 20% dos casos sairá bola amarela. Quanto maior a quantidade de experimentos, tanto mais a distribuição do número de ocorrências se aproximará dos percentuais indicados.
Propriedades da probabilidade de um evento
P1: A probabilidade do evento impossível é nula.Com efeito, sendo o evento impossível o conjunto vazio (Ø), teremos:
p(Ø) = n(Ø)/n(U) = 0/n(U) = 0
Por exemplo, se numa urna só existem bolas brancas, a probabilidade de se retirar uma bola verde (evento impossível, neste caso) é nula.
P2: A probabilidade do evento certo é igual a unidade.
Com efeito, p(A) = n(U)/n(U) = 1
Por exemplo, se numa urna só existem bolas vermelhas, a probabilidade de se retirar uma bola vermelha (evento certo, neste caso) é igual a 1.
P3: A probabilidade de um evento qualquer é um número real situado no intervalo real [0, 1].
Esta propriedade, decorre das propriedades 1 e 2 acima.
P4: A soma das probabilidades de um evento e do seu evento complementar é igual a unidade.Seja o evento A e o seu complementar A'. Sabemos que A U A' = U.
n(A U A') = n(U) e, portanto, n(A) + n(A') = n(U).
Dividindo ambos os membros por n(U), vem:
n(A)/n(U) + n(A')/n(U) = n(U)/n(U), de onde conclui-se:
p(A) + p(A') = 1
Nota: esta propriedade simples, é muito importante pois facilita a solução de muitos problemas aparentemente complicados. Em muitos casos, é mais fácil calcular a probabilidade do evento complementar e, pela propriedade acima, fica fácil determinar a probabilidade do evento.
P5: Sendo A e B dois eventos, podemos escrever:
p(A U B) = p(A) + p(B) – p(A Ç B)Observe que se A ÇB= Ø (ou seja, a interseção entre os conjuntos A e B é o conjunto vazio), então p(A U B) = p(A) + p(B).
Com efeito, já sabemos da Teoria dos Conjuntos que
n(A U B) = n(A) + n(B) – n(A ÇB)
Dividindo ambos os membros por n(U) e aplicando a definição de probabilidade, concluímos rapidamente a veracidade da fórmula acima.
Exemplo:
Em uma certa comunidade existem dois jornais J e P. Sabe-se que 5000 pessoas são assinantes do jornal J, 4000 são assinantes de P, 1200 são assinantes de ambos e 800 não lêem jornal. Qual a probabilidade de que uma pessoa escolhida ao acaso seja assinante de ambos os jornais?
SOLUÇÃO:
Precisamos calcular o número de pessoas do conjunto universo, ou seja, nosso espaço amostral. Teremos:
n(U) = N(J U P) + N.º de pessoas que não lêem jornais.
n(U) = n(J) + N(P) – N(J ÇP) + 800
n(U) = 5000 + 4000 – 1200 + 800
n(U) = 8600
Portanto, a probabilidade procurada será igual a:
p = 1200/8600 = 12/86 = 6/43.
Logo, p = 6/43 = 0,1395 = 13,95%.
A interpretação do resultado é a seguinte: escolhendo-se ao acaso uma pessoa da comunidade, a probabilidade de que ela seja assinante de ambos os jornais é de aproximadamente 14%.(contra 86% de probabilidade de não ser).
Probabilidade condicional - conceito e exemplos
.A probabilidade condicional trata da probabilidade de ocorrer um evento A, tendo ocorrido um evento B, ambos do espaço amostral S, ou seja, ela é calculada sobre o evento B e não em função o espaço amostral S.
Exemplo 2:
Uma urna possui cinco bolas vermelhas e duas bolas brancas.
Calcule as probabilidades de:
a) em duas retiradas, sem reposição da primeira bola retirada, sair uma bola vermelha (V) e depois uma bola branca (B).
Solução:
p(V Ç B) = p(V) . p(B/V)
p(V) = 5/7 (5 bolas vermelhas de um total de 7).
Supondo que saiu bola vermelha na primeira retirada, ficaram 6 bolas na urna. Logo:
p(B/V) = 2/6 = 1/3
Da lei das probabilidades compostas, vem finalmente que:
P(V Ç B) = 5/7 . 1/3 = 5/21 = 0,2380 = 23,8%
b) em duas retiradas, com reposição da primeira bola retirada, sair uma bola vermelha e depois uma bola branca.
Solução:
Com a reposição da primeira bola retirada, os eventos ficam independentes. Neste caso, a probabilidade buscada poderá ser calculada como:
P(V Ç B) = p(V) . p(B) = 5/7 . 2/7 = 10/49 = 0,2041 = 20,41%
Observe atentamente a diferença entre as soluções dos itens (a) e (b) acima, para um entendimento perfeito daquilo que procuramos transmitir.
Exemplo 3:
Em uma pesquisa realizada com 10.000 consumidores sobre a preferência da marca de sabão em pó, verificou-se que: 6500 utilizam a marca X; 5500 utilizam a marca Y; 2000 utilizam as duas marcas. Foi sorteada uma pessoa desse grupo e verificou-se que ela utiliza a marca X. Qual a probabilidade dessa pessoa ser também usuária da marca Y?
Solução: Vamos identificar cada um dos eventos.
A: Usuário da marca Y.
B: Usuário da marca X.
Queremos determinar P(A|B) e sabemos que o número de elementos do espaço amostral é n(S) = 10000.
Temos, também, que:
n(A∩B) = 2000
Segue que:
Mas
Da teoria de conjunto, temos que:
n(B) = 6500 – n(A∩B) = 6500 – 2000 = 4500
Assim, teremos:
Logo,
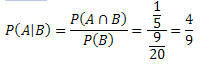
Questões resolvidas de vestibulares sobre probabilidade
1) Três estudantes A, B e C estão em uma competição de natação. A e B têm as mesmas chances de vencer e, cada um, tem duas vezes mais chances de vencer do que C. Pede-se calcular a probabilidades de A ou C vencer.
Solução:
Sejam p(A), p(B) e p(C), as probabilidades individuais de A, B, C, vencerem. Pelos dados do enunciado, temos:
p(A) = p(B) = 2.p(C).
Seja p(A) = k. Então, p(B) = k e p(C) = k/2. Temos: p(A) + p(B) + p(C) = 1.
Isto é explicado pelo fato de que a probabilidade de .A vencer ou B vencer ou C vencer é igual a (evento certo).
Assim, substituindo, vem:
k + k + k/2 = 1 \ k = 2/5. Portanto, p(A) = k = 2/5, p(B) = 2/5 e p(C) = 2/10 = 1/5.
A probabilidade de A ou C vencer será a soma dessas probabilidades, ou seja 2/5 + 1/5 = 3/5.
2) Um cartão é retirado aleatoriamente de um conjunto de 50 cartões numerados de 1 a 50. Determine a probabilidade do cartão retirado ser de um número primo.
Solução:
Os números primos de 1 a 50 são: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 e 47, portanto, 15 números primos.
Temos, portanto, 15 chances de escolher um número primo num total de 50 possibilidades. Portanto, a probabilidade pedida será igual a p = 15/50 = 3/10.
3) Alguns amigos estão em uma lanchonete. Sobre a mesa há duas travessas. Em uma delas há 3 pastéis e 5 coxinhas. Na outra há 2 coxinhas e 4 pastéis. Se ao acaso alguém escolher uma destas travessas e também ao acaso pegar um dos salgados, qual a probabilidade de se ter pegado um pastel?
Solução:
A probabilidade de escolhermos 1 dentre 2 travessas é igual 1/2.
A probabilidade de escolhermos um pastel na primeira travessa é 3 em 8, ou seja, é 3/8 e como a probabilidade de escolhermos a primeira travessa é 1/2, temos:
A probabilidade de escolhermos um pastel na segunda travessa é 4 em 6, isto é 4/6 e como a probabilidade de escolhermos a segunda travessa é igual a 1/2, temos:
Então a probabilidade de escolhermos um pastel é igual a:
A probabilidade de se ter pegado um pastel é 25/48.
4) O jogo de dominó é composto de peças retangulares formadas pela junção de dois quadrados. Em cada quadrado há a indicação de um número, representado por uma certa quantidade de bolinhas, que variam de nenhuma a seis. O número total de combinações possíveis é de 28 peças. Se pegarmos uma peça qualquer, qual a probabilidade dela possuir ao menos um 3 ou 4 na sua face?
Solução:
Chamemos de A o evento da ocorrência de um 3:
A = { (0, 3), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (6, 3) }
Chamemos de B o evento da ocorrência de um 4:
B = { (4, 0), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6) }
Veja que o elemento (4, 3) integra os dois eventos, logo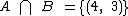 
.
Calculando as probabilidades de A, B e da intersecção, temos:
Finalmente para o cálculo da probabilidade desejada vamos utilizar a fórmula da probabilidade da união de dois eventos:
Repare que 13 é o número total de peças que possuem 3 ou 4, desconsiderando-se a ocorrência que se repete (o (4 ,3) da intersecção dos dois eventos).
A probabilidade de ela possuir ao menos um 3 ou 4 na sua face é 13/28.
5) Em uma escola de idiomas com 2000 alunos, 500 alunos fazem o curso de inglês, 300 fazem o curso de espanhol e 200 cursam ambos os cursos. Selecionando-se um estudante do curso de inglês, qual a probabilidade dele também estar cursando o curso de espanhol?
Solução:
Chamemos de A o evento que representa o curso de espanhol e B o evento que representa o curso de inglês.
Podemos calcular a probabilidade de ocorrer A tendo ocorrido B através da fórmula:
Segundo o enunciado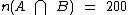 
e 
, e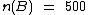ntão:
Note que no caso da probabilidade condicional, ao invés de calcularmos a probabilidade em função do número de elementos do espaço amostral, a calculamos em função do número de elementos do evento que já ocorreu.
A probabilidade do aluno também estar cursando o curso de espanhol é 2/5.
6) Em uma caixa há 2 fichas amarelas, 5 fichas azuis e 7 fichas verdes. Se retirarmos uma única ficha, qual a probabilidade dela ser verde ou amarela?
Solução:
Na parte teórica vimos que a probabilidade da união de dois eventos pode ser calculada através da fórmula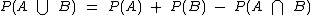 
e no caso da intersecção dos eventos ser vazia, isto é, não haver elementos em comum aos dois eventos, podemos simplesmente utilizar 
.
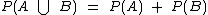Ao somarmos a quantidade de fichas obtemos a quantidade 14. Esta quantidade é o número total de elementos do espaço amostral.
Neste exercício os eventos obter ficha verde e obter ficha amarela são mutuamente exclusivos, pois a ocorrência de um impede a ocorrência do outro, não há elementos que fazem parte dos dois eventos. Não há bolas verdes que são também amarelas. Neste caso então podemos utilizar a fórmula:
Note que esta fórmula nada mais é que a soma da probabilidade de cada um dos eventos.
O evento de se obter ficha verde possui 7 elementos e o espaço amostral possui 14 elementos, que é o número total de fichas, então a probabilidade do evento obter ficha verde ocorrer é igual a 7/14:
Analogamente, a probabilidade do evento obter ficha amarela, que possui 2 elementos, é igual a 2/14:
Observe que poderíamos ter simplificado as probabilidades, quando então 7/14 passaria a 1/2 e 2/14 a 1/7, no entanto isto não foi feito, já que para somarmos as duas probabilidades precisamos que elas tenham um denominador comum:
Este exercício foi resolvido através da fórmula da probabilidade da união de dois eventos para que você tivesse um exemplo da utilização da mesma e pudesse aprender quando utilizá-la, mas se você prestar atenção ao enunciado, poderá ver que poderíamos tê-lo resolvido de uma outra forma, que em alguns casos pode tornar a resolução mais rápida. Vejamos:
Note que a probabilidade de se obter ficha azul é 5 em 14, ou seja, 5/14. Então a probabilidade de não se obter ficha azul é 9 em 14, pois:
O 1 que aparece na expressão acima se refere à probabilidade do espaço amostral.
Note que utilizamos o conceito de evento complementar, pois se não tivermos uma ficha azul, só poderemos ter uma ficha verde ou uma ficha amarela, pois não há outra opção.
A probabilidade de ela ser verde ou amarela é 9/14.
7) De uma sacola contendo 15 bolas numeradas de 1 a 15 retira-se uma bola. Qual é a probabilidade desta bola ser divisível por 3 ou divisível por 4?
Solução:
Vamos representar por E3 o evento da ocorrência das bolas divisíveis por 3:
E3 = { 3, 6, 9, 12, 15 }
E por E4 vamos representar o evento da ocorrência das bolas divisíveis por 4:
E4 = { 4, 8, 12 }
O espaço amostral é:
S = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 }
A probabilidade de sair uma bola divisível por 3 é:
A probabilidade de sair uma bola divisível por 4 é:
Como estamos interessados em uma ocorrência ou em outra, devemos somar as probabilidades, mas como explicado no tópico união de dois eventos, devemos subtrair a probabilidade da intersecção, pois tais eventos não são mutuamente exclusivos. Como podemos ver, o número 12 está contido tanto em E3 quanto em E4, ou seja:
A probabilidade da intersecção é:
Portanto:
A probabilidade desta bola ser divisível por 3 ou divisível por 4 é 7/15.
8) Uma moeda é viciada, de forma que as coroas são cinco vezes mais prováveis de aparecer do que as caras. Determine a probabilidade de num lançamento sair coroa.
Solução:
5/6 = 83,33%
9) Num clube desportivo 30 meninos praticam futebol. Doze treinam para o ataque, quinze para a defesa e cinco para goleiro.
Qual é a probabilidade de escolhendo um desportista ao acaso ele treinar para a defesa e o ataque?
Solução:
Para ajudar vamos fazer um esquema:
 | 30 - 5 = 25 ...... Não treinam para goleiro.
12 + 15 = 27 ... Treinam para defesa ou ataque.
27 - 25 = 2 ...... Treinam para defesa e ataque.Casos favoráveis: 2
Casos possíveis: 30
Logo, P = 2/30 = 1/15 |
10) Extrai-se ao acaso uma bola de uma caixa que contém 6 bolas vermelhas, 4 brancas e 5 azuis. Determine a probabilidade de a bola extraída ser:
(a) vermelha;
Temos que,
(b) vermelha ou branca;
Temos que,
11) No lançamento de dois dados, calcule a probabilidade de se obter soma igual a 5.
Solução:
Casos possíveis: 36
Casos favoráveis: (1+4, 2+3, 3+2, 4+1) 4
Probabilidade: 4/36
12) (CESGRANRIO/PETROBRAS/ENGENHEIRO DE PRODUÇÃO JR/2011/FEVEREIRO)
Um estudo sobre fidelidade do consumidor à operadora de telefonia móvel, em uma determinada localidade, mostrou as seguintes probabilidades sobre o hábito de mudança:
A probabilidade de o 1º telefone de um indivíduo ser da operadora A é 0,60; a probabilidade de o 1o telefone ser da operadora B é de 0,30; e a de ser da operadora C é 0,10. Dado que o 2o telefone de um cliente é da operadora A, a probabilidade de o 1o também ter sido é de
(A) 0,75
(B) 0,70
(C) 0,50
(D) 0,45
(E) 0,40
Solução:
Temos uma questão de probabilidade condicional que pode ser identificada na pergunta: Dado que o 2o telefone de um cliente é da operadora A, a probabilidade de o 1o também ter sido é de.
O condicionamento reduz o espaço amostral.
Dados do enunciado:
P(1°A) = 0,6
P(1°B) = 0,3
P(1°C) = 0,1
Então usando a fórmula de probabilidade condicional de Bayes:
P(1°A/2°A) = [P(1°A) x P(2°A/1°A)] / [P(1°A) x P(2°A/1°A) + P(1°B) x P(2°A/1°B) + P(1°C) x P(2°A/1°C)]
P(1°A/2°A) = [0,6 x 0,5] / [0,6 x 0,5 + 0,3 x 0,2 + 0,1 x 0,4] = 0,75
Gabarito letra A
13) Um jogo consiste em lançar uma moeda honesta até obter duas caras consecutivas ou duas coroas consecutivas. Na primeira situação, ao obter duas caras consecutivas, ganha-se o jogo. Na segunda, ao obter duas coroas consecutivas, perde-se o jogo. A probabilidade de que o jogo termine, com vitória, até o sexto lance, é
(A) 7/16
(B) 31/64
(C) 1/2
(D) 1/32
(E) 1/64
Solução:
Para resolver essa questão montamos um quadro:
Como está pedindo a probabilidade de vitória até o sexto lance, o jogo pode terminar com vitória do 2° ao 6° lance.
A probabilidade será a soma de todas essas probabilidades, pois o jogo pode terminar com vitória no 2° ou 3° ou 4° ou 5° ou 6° lances.
= ¼ + 1/8 + 1/16 + 1/32 + 1/64 = 31/64
Gabarito letra B
14) (CESGRANRIO/PETROBRAS/ENG DE PRODUÇÃO/2005) Uma determinada fábrica produz peças tipo A e B nas proporções 1/3 e 2/3, respectivamente. A probabilidade de ocorrência da peça defeituosa do tipo A é de 20% e do tipo B é 10%. Retirando-se, ao acaso, uma peça produzida na fábrica, a probabilidade de ela de ser defeituosa é de:
(A) 1/30
(B) 1/15
(C) 1/10
(D) 1/6
(E) 2/15
Solução:
Probabilidade de ser do tipo A = 1/3
Probabilidade de ser do tipo B = 2/3
Prob. Def. A = 0,2
Prob. Def. B = 0,1
A probabilidade da peça ser defeituosa é a probabilidade da peça ser do tipo A Edefeituosa OU ser do tipo B E defeituosa.
Sabe-se que E implica em multiplicação e OU implica em adição.
Probabilidade da peça ser do tipo A E defeituosa = (1/3)x(0,2) = 1/15
Probabilidade da peça ser do tipo B E defeituosa = (2/3) x (0,1) = 1/15
Então, a probabilidade da peça ser defeituosa é (1/15) + (1/15) = 2/15
Gabarito letra E.
15) Um grupo de amigos contém 5 torcedores do São Paulo, 4 torcedores do Flamengo, 2 torcedores do Grêmio e 1 torcedor do Bahia. Calcule as possibilidades:
a) Sortearmos um torcedor do Flamengo:
P = 4/12 = 1/3 = 0,3333 ou 33,33%
b) Sortearmos um torcedor do São Paulo ou do Bahia:
P = 6/12 = 1/2 = 0,5 ou 50%
c) Sortearmos os dois torcedores do Grêmio:
P = 2/12 x 1/11 = 1/66 = 0,01515 ou 1,5151%
d) Sortearmos dois torcedores do São Paulo:
P = 5/12 x 4/11 = 0,1515 = 15,15%
16) Um casal planeja ter 5 filhos. Qual a probabilidade de nascerem 3 meninos e 2 meninas?
Solução:
Primeiramente, devemos observar que não importa a ordem de nascimento, assim, temos 6 opções:
- 5 meninos
- 4 meninos e 1 menina
- 3 meninos e 2 meninas
- 2 meninos e 3 meninas
- 1 menino e 4 meninas
- 5 meninas
Logo, a probabilidade de nascerem 3 meninos e 2 meninas é:
P = 1/6 = 0,1666 = 16,66%
17) (Fundação Carlos Chagas - Escriturário BB - 2011) Para disputar a final de um torneio internacional de natação, classificaram-se 8 atletas: 3 norte-americanos, 1 australiano, 1 japonês, 1 francês e 2 brasileiros. Considerando que todos os atletas classificados são ótimos e têm iguais condições de receber uma medalha (de ouro, prata ou bronze), a probabilidade de que pelo menos um brasileiro esteja entre os três primeiros colocados é igual a:
Dica: Quando aparecer na questão `pelo menos um`, devemos encontrar a probabilidade de não acontecer nenhum, ou seja, de não termos brasileiros no pódio, e depois diminuirmos de 1.
Probabilidades:
De nenhum brasileiro ganhar ouro = 6/8 = 3/4
De nenhum brasileiro ganhar prata = 5/7 (desconsideramos a medalha de ouro)
De nenhum brasileiro ganhar bronze = 4/6 = 2/3 (desconsideramos as medalhas de ouro ou prata)
Então:
P (não termos brasileiros no pódio) = 3/4 x 5/7 x 2/3 = 5/14
P (termos pelo menos um brasileiro no pódio) = 1 - 5/14 = 14/14 - 5/14 = 9/14
18) (CESGRANRIO - BB 2012) Uma moeda não tendenciosa é lançada até que sejam obtidos dois resultados consecutivos iguais. Qual a probabilidade de a moeda ser lançada exatamente três vezes?
(A) 1/8
(B) 1/4
(C) 1/3
(D) 1/2
(E) 3/4
Solução:
Primeira jogada: qualquer resultado serve (probabilidade 1)
Segunda jogada: só serve o resultado que não aconteceu da segunda vez (probabilidade ½)
Terceira jogada: só serve o mesmo resultado da segunda jogada (probabilidade ½)
Logo: 1 x ½ x ½ = ¼
19) (Sefaz/PI – Agente Fiscal de Tributos Estaduais – ESAF – 2001) De dez contas de um arquivo, quatro contêm erro de apropriação. Se um auditor seleciona, aleatoriamente e sem reposição, duas contas entre as dez, a probabilidade de que apenas uma das contas selecionadas contenha erro de apropriação é igual a:
a) 13,3% b) 23,3% c) 33,3% d) 43,3% e) 53,3%
Solução:
Abaixo separamos os grupos de contas (com erro e sem erro).
10 contas, sendo 4 contas com erro e 6 contas sem erro.
A tabela abaixo foi montada seguindo o critério de que uma conta só pode ter o status (com erro ou sem erro) e, como serão duas seleções sem reposição, se o auditor selecionar uma conta com erro (numa primeira tentativa) devemos representar da seguinte forma
| | SELEÇÃO 1 | SELEÇÃO 2 | RESULTADO |
TE
N
T
A
T
I
V
A
1 | 1ª conta selecionada pelo auditor pode ser | 2ª conta selecionada pelo auditor pode ser | Possibilidade primeiro com erro e segundo sem erro |
| ComErro | 4/10 | SemErro | 6/9 | 4/10 x 6/9 = 24/90Tentativa 1 |
| (na primeira seleção existem 4 possibilidades em 10 da conta estar com erro) | (na segunda seleção existem 6 possibilidades em 9 da conta estar sem erro, pois já foi retirada uma conta do arquivo na seleção anterior) | |
| | Tentativa 1 + Tentativa 2 |
TE
N
T
A
T
I
V
A
2 | 1ª conta selecionada pelo auditor pode ser | 2ª conta selecionada pelo auditor pode ser | Possibilidade primeiro com sem e segundo com erro |
| SemErro | 6/10 | ComErro | 4/9 | 6/10 x 4/9 =24/90Tentativa 2 |
| (na primeira seleção existem 6 possibilidades em 10 da conta estar semerro) | (na segunda seleção existem 6 possibilidades em 9 da conta estar sem erro, pois já foi retirada uma conta do arquivo na seleção anterior) | |
| | Ou (somar tentativas encontradas) | = 24/90 + 24/90 = 53,3% |
Alternativa E
20) (Assessor Legislativo-PA) Um Shopping Center possui dois sistemas automáticos de proteção contra incêndios. A eficiência de cada sistema, segundo o fabricante, é de 99%. Sabendo-se que os sistemas funcionam de modo totalmente independente e que ambos permanecem ligados 24 horas por dia, qual é a probabilidade de que um incêndio seja detectado e neutralizado?
A) 99,99%
B) 99,00%
C) 98,01%
D) 97,00%
E) 96,66%
Solução:
Nessa questão, devemos lembrar o conceito de eventos ou sistemas independentes. Na figura abaixo, imaginemos 3 eventos independentes. Nesse caso, percebemos que a ocorrência de um não exclui a do outro, e vice-versa. Em eventos independentes, há ocorrência simultânea, sem problemas!
Na questão dada, a eficiência individual de cada um dos sistemas de proteção contra incêndios é de 99%. Ou seja, a chance de que cada um venha a falhar é de 1% (100% – 99%). Ou o sistema funciona, ou falha! Desse modo, a chance de que os dois venham a falhar será de 1% x 1%. Uma chance pequena, convenhamos. (1/100) x (1/100) = 1/10.000, que fica em 0,0001. Multiplicamos esse valor por 100, e teremos a forma percentual de que os dois sistemas falhem: 0,01%. Somente nesse caso vai dar furo no sistema de segurança do Shopping Center. Em quaisquer outras circunstâncias, o sistema detectará um possível incêndio. Então, para sabermos a probabilidade de que um incêndio seja detectado e neutralizado, basta fazermos 100% – 0,01% = 99,99%. Somente 0,01% não pode ocorrer, o resto pode!. Letra A.
21) (PETROBRAS-2012.1) Sabe-se por estudos estatísticos que as probabilidades de haver num certo almoxarifado os materiais A, B e C disponíveis para uso são de, respectivamente, 80%, 80% e 90%.
Qual é a probabilidade de, num dado momento, estar faltando pelo menos um desses materiais no almoxarifado?
Solução:
Calcule a chance de terem todos, ou seja:
0,8 * 0,8 * 0,9 = 0,576 = 57,6% de terem os tres ao mesmo tempo.
A chance de estar faltando pelo menos um, é o total menos a chance de ter todos:
P(falta) = 100% - 57,6%
P(falta) = 42,4%
22) (UFSCar) Dois dados usuais e não viciados são lançados. Sabe-se que os números observados são ímpares. Então, a probabilidade de que a soma deles seja 8 é:
a) 2/36
b) 1/6
c) 2/9
d) 1/4
e) 2/18
Solução:
No lançamento de dois dados temos que a soma entre as faces ímpares em que o resultado seja 8 é dado pelos pares (5, 3) e (3, 5). Somente 2 eventos dos 36 pertencentes ao espaço amostral satisfazem a situação proposta. Portanto:
Temos que o item a fornece a resposta correta.
23) (FUVEST) Um dado cúbico, não viciado, com faces numeradas de 1 a 6, é lançado três vezes. Em cada lançamento, anota-se o número obtido na face superior do dado, formando-se uma sequência (a, b, c). Qual é a probabilidade de que b seja sucessor de a ou que c seja sucessor de b
?
a) 4/27
b) 11/54
c) 7/27
d) 10/27
e) 23/54
24) (FGV) Uma urna contém cinco bolas numeradas com 1, 2, 3, 4 e 5. Sorteando-se ao acaso, e com reposição, três bolas, os números obtidos são representados por x, y e z . A probabilidade de que xy + z seja um número par é de
(A) 47/125
(B) 2/5
(C) 59/125
(D) 64/125
(E) 3/5
25) (PUCCAMP) Numa certa população são daltônicos 5% do total de homens e 0,05% do total de mulheres. Sorteando-se ao acaso um casal dessa população, a probabilidade de ambos serem daltônicos é
(A) 1/1.000.
(B) 1/10.000.
(C) 1/20.000.
(D) 1/30.000.
(E) 1/40.000.
26) (ESPM) Uma urna contém 1 bola branca, 1 bola preta e 8 bolas verdes, distinguíveis apenas pela cor. Essas bolas vão sendo retiradas uma a uma, aleatoriamente e sem retorno, observando-se suas cores. A probabilidade de que a cor branca seja a primeira cor a se esgotar nessa urna é de:
a) 22/45.
b) 43/90.
c) 49/100.
d) 12/25.
e) 7/15.
27) (PUC-03) De sua turma de 30 alunos, é escolhida uma comissão de 3 representantes. Qual a probabilidade de você fazer parte da comissão?
A) 1/10
B) 1/12
C) 5/24
D) 1/3
E) 2/9
28) Uma carta é retirada de um baralho comum, de 52 cartas, e, sem saber qual é a carta, é misturada com as cartas de um outro baralho idêntico ao primeiro. Retirando, em seguida, uma carta do segundo baralho, a probabilidade de se obter uma dama é:
A) 3/51
B) 5/53
C) 5/676
D) 1/13
E) 5/689
29) Três pessoas A, B e C vão participar de um concurso num programa de televisão. O apresentador faz um sorteio entre A e B e, em seguida, faz um sorteio, para decidir quem iniciará o concurso. Se em cada sorteio as duas pessoas têm a mesma "chance" de ganhar, qual é a probabilidade de A iniciar o concurso?
A) 12,5%
B) 25%
C) 50%
D) 75%
E) 95%
30) (UNI- RIO) As probabilidades de três jogadores marcarem um gol cobrando pênalti são, respectivamente, 1/2, 2/5, e 5/6. Se cada um bater um único pênalti, a probabilidade de todos errarem é igual a:
a) 3%
b) 5%c) 17%
d) 20%
e) 25%
31) (GV) Cada dia em que uma pessoa joga numa loteria, ela tem uma probabilidade de ganhar igual a 1/1000, independentemente dos resultados anteriores.
a) Se ela jogar 30 dias, qual a probabilidade de ganhar ao menos uma vez?
1 - (0,999)30
b) Qual o número mínimo de dias em que ele deverá jogar para que a probabilidade de que ela ganhe ao menos uma vez seja maior do que 0,3%?
o menor número inteiro n tal que n > log0,9990,997.
32) Numa pesquisa sobre preferência entre dois refrigerantes, Coca-Cola e guaraná, obtivemos o seguinte resultado:
20 tomam guaraná
15 tomam Coca-Cola
08 tomam os dois
03 não tomam nenhum dos dois.
Sorteando-se uma pessoa ao acaso, calcule a probabilidade de ela tomar guaraná ou Coca-Cola?
a) 5/6
b) 10/5
c) 10/6
d) 5/3
e) 5/12
33) Lançado simultaneamente dois dados, qual a probabilidade de que a soma seja 7?
a) 32%
b) 16,66%
c) 32,22%
d) 8,88%
e) 28,88%
.jpg)
.jpg)
.gif)
.gif)
