Triângulo de Pascal
O triângulo de Pascal é um triângulo aritmético formado por números que têm diversas relações entre si. Muitas dessas relações foram descobertas pelo próprio Pascal, o que justifica o nome que lhe é dado.
NOTA: Considera-se que o topo do triângulo corresponde à linha 0, coluna 0.
Apresentando a fórmula matemática para esta propriedade:
 sendo n o número de linhas e k o número de colunas dessa linha onde o número está (não se conta com o topo do triângulo, pois numa sucessão definida por recorrência tem que existir uma condição inicial, tal é 1).
sendo n o número de linhas e k o número de colunas dessa linha onde o número está (não se conta com o topo do triângulo, pois numa sucessão definida por recorrência tem que existir uma condição inicial, tal é 1).
Tal fórmula prova-se por indução matemática em n.
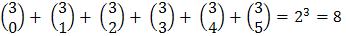
Binômio de Newton
Denomina-se Binômio de Newton, a todo binômio da forma (a + b)n , sendo n um número natural, que é chamado de ordem do binômio.
Assim, para determinar quais são as combinações possíveis quando uma distribuição possui os parâmetros p e q, faz-se a expansão do
Binômio de Newton: : (p + q)n
Quando o expoente n for 2, fica simples, apenas decorando “o quadrado do primeiro mais duas vezes o primeiro pelo segundo mais o quadrado do segundo” = (a + b)2 = a2 + 2ab + b2 . Porém quando o expoente for um número maior, fica mais complicado, do que aplicar o método da distributiva (“chuveirinho”).
A fórmula que Newton criou é a seguinte:
O numero de termos da nova expressão será o expoente n + 1 .
Exemplo de utilização do binômio de Newton

Para saber rapidamente quais são os valores dos números binomiais, basta pesquisarmos o Triângulo de Pascal:

Então obtemos a expressão:
1.16x4.1 + 4.8x3.1 + 6.4x2.1 + 4.2x . 1 + 1.1.1
1.16x4.1 + 32x3.1 + 24x2.1 + 8x . 1 + 1
Caso em uma questão de vestibular seja pedido a soma dos coeficientes numérico do desenvolvimento de um binômio, não é necessário fazer todo o desenvolvimento pelo binômio de newton, basta saber a seguinte dica:
- troque qualquer letra do binômio por 1
- calcule o valor que ficará dentro dos parênteses, e pronto, basta elevá-lo à n.
No desenvolvimento que mostramos anteriormente, a soma dos coeficientes é 81 (16 + 32 + 24 + 8 + 1), agora utilizando a dica dada:
(2x+1)4
(2.1 + 1)4 = 34 = 81
Observações:
1) o desenvolvimento do binômio (a + b)n é um polinômio.
2) o desenvolvimento de (a + b)n possui n + 1 termos .
3) os coeficientes dos termos equidistantes dos extremos , no desenvolvimento de
(a + b)n são iguais .
4) a soma dos coeficientes de (a + b)n é igual a 2n .
Questões resolvidas sobre Triângulo de Pascal e Binômio de Newton
1) Qual o termo médio do desenvolvimento de (2x + 3y)8 ?
2) Determine o 7º termo do binômio (2x + 1)9 , desenvolvido segundo as potências decrescentes de x.



O triângulo de Pascal é um triângulo aritmético formado por números que têm diversas relações entre si. Muitas dessas relações foram descobertas pelo próprio Pascal, o que justifica o nome que lhe é dado.
| 1 | ||||||||||||||
| 1 | 1 | |||||||||||||
| 1 | 2 | 1 | ||||||||||||
| 1 | 3 | 3 | 1 | |||||||||||
| 1 | 4 | 6 | 4 | 1 | ||||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
...
Este triângulo forma-se de forma recursiva, ou seja, as diagonais de fora são formadas por 1's, os restantes números são a soma dos números acima. Como exemplo podemos dizer que: 10=4+6 (10-linha 5; 4 e 6-linha 4).NOTA: Considera-se que o topo do triângulo corresponde à linha 0, coluna 0.
Apresentando a fórmula matemática para esta propriedade:

Tal fórmula prova-se por indução matemática em n.
 Propriedades do Triângulo de Pascal
As propriedades do triângulo de Pascal são as seguintes:
Cada linha representa os números binomiais na expansão de (x+y)n, n≥0. Por exemplo,
(x+y)3=1.x3 + 3x2y + 3xy2 + 1.y3 e na quarta linha temos 1 3 3 1.
Ocorre que sabemos pelo Binômio de Newton que cada número do triângulo de Pascal será um coeficiente binomial, ou seja, na (n+1)-ésima linha o (k+1)-ésimo número será:
Por exemplo, na 5ª linha o terceiro número é:
Pela construção do triângulo de Pascal, temos:
Por exemplo, 10=4+6, ou seja:
A soma de todos os números na (n+1)-ésima linha é igual a 2n. Por exemplo, na 1ª linha a soma é 20=1, na 4ª linha 23=8, etc.
O triângulo de Pascal é simétrico em relação a sua altura pois
Se somarmos a diagonal também temos o seguinte resultado:
Por exemplo, na 3ª diagonal: 1+3+6+10=20, ou
|
Vamos resolver os seguintes exemplos, aplicando as propriedades do triângulo de Pascal.
Exemplo 1:
Sendo 1 a 21 35 b c 7 1 uma linha do triângulo de Pascal, determinar a, b e c:
Solução:
1 a 21 35 b c 7 1
Pela 1ª propriedade, temos a = 7, b = 35 e c = 21.
Exemplo 2:
Sendo:
1 7 21 b 35 21 e 1
1 8 a 56 c d 28 8 1
duas linhas consecutivas do triângulo de Pascal, vamos determinar a, b, c, d, e.
De acordo com a 2ª propriedade, temos:
a = 7 + 21 = 28
21 + b = 56 ► b = 35
b + 35 = c ► c = 70
d = 35 + 21 = 56
21 + e = 28 ► e = 7
Calcular a soma:
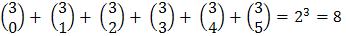
Denomina-se Binômio de Newton, a todo binômio da forma (a + b)n , sendo n um número natural, que é chamado de ordem do binômio.
Assim, para determinar quais são as combinações possíveis quando uma distribuição possui os parâmetros p e q, faz-se a expansão do
Binômio de Newton: : (p + q)n
Quando o expoente n for 2, fica simples, apenas decorando “o quadrado do primeiro mais duas vezes o primeiro pelo segundo mais o quadrado do segundo” = (a + b)2 = a2 + 2ab + b2 . Porém quando o expoente for um número maior, fica mais complicado, do que aplicar o método da distributiva (“chuveirinho”).
A fórmula que Newton criou é a seguinte:

O numero de termos da nova expressão será o expoente n + 1 .
Exemplo de utilização do binômio de Newton

Para saber rapidamente quais são os valores dos números binomiais, basta pesquisarmos o Triângulo de Pascal:

Então obtemos a expressão:
1.16x4.1 + 4.8x3.1 + 6.4x2.1 + 4.2x . 1 + 1.1.1
1.16x4.1 + 32x3.1 + 24x2.1 + 8x . 1 + 1
Caso em uma questão de vestibular seja pedido a soma dos coeficientes numérico do desenvolvimento de um binômio, não é necessário fazer todo o desenvolvimento pelo binômio de newton, basta saber a seguinte dica:
- troque qualquer letra do binômio por 1
- calcule o valor que ficará dentro dos parênteses, e pronto, basta elevá-lo à n.
No desenvolvimento que mostramos anteriormente, a soma dos coeficientes é 81 (16 + 32 + 24 + 8 + 1), agora utilizando a dica dada:
(2x+1)4
(2.1 + 1)4 = 34 = 81
Observações:
1) o desenvolvimento do binômio (a + b)n é um polinômio.
2) o desenvolvimento de (a + b)n possui n + 1 termos .
3) os coeficientes dos termos equidistantes dos extremos , no desenvolvimento de
(a + b)n são iguais .
4) a soma dos coeficientes de (a + b)n é igual a 2n .
Fonte: www.algosobre.com.br/
Questões resolvidas sobre Triângulo de Pascal e Binômio de Newton
1) Qual o termo médio do desenvolvimento de (2x + 3y)8 ?
Solução:Temos a = 2x , b = 3y e n = 8. Sabemos que o desenvolvimento do binômio terá 9 termos, porque n = 8. Ora sendo T1 T2 T3 T4 T5 T6 T7 T8 T9 os termos do desenvolvimento do binômio, o termo do meio (termo médio) será o T5 (quinto termo). Logo, o nosso problema resume-se ao cálculo do T5 . Para isto, basta fazer
p = 4 na fórmula do termo geral e efetuar os cálculos decorrentes.
Teremos:
T4+1 = T5 = C8,4 . (2x)8-4 . (3y)4 = 8! / [(8-4)! . 4!] . (2x)4 . (3y)4
= 8.7.6.5.4! / (4! . 4.3.2.1) . 16x4.81y4
Fazendo as contas vem:
T5 = 70.16.81.x4 . y4 = 90720x4y4 , que é o termo médio procurado.
p = 4 na fórmula do termo geral e efetuar os cálculos decorrentes.
Teremos:
T4+1 = T5 = C8,4 . (2x)8-4 . (3y)4 = 8! / [(8-4)! . 4!] . (2x)4 . (3y)4
= 8.7.6.5.4! / (4! . 4.3.2.1) . 16x4.81y4
Fazendo as contas vem:
T5 = 70.16.81.x4 . y4 = 90720x4y4 , que é o termo médio procurado.
Solução:Vamos aplicar a fórmula do termo geral de (a + b)n , onde a = 2x , b = 1 e n = 9. Como queremos o sétimo termo, fazemos p = 6 na fórmula do termo geral e efetuamos os cálculos indicados. Temos então:
T6+1 = T7 = C9,6 . (2x)9-6 . (1)6 = 9! /[(9-6)! . 6!] . (2x)3 . 1 = 9.8.7.6! / 3.2.1.6! . 8x3 = 84.8x3= 672x3. Portanto o sétimo termo procurado é 672x3.
T6+1 = T7 = C9,6 . (2x)9-6 . (1)6 = 9! /[(9-6)! . 6!] . (2x)3 . 1 = 9.8.7.6! / 3.2.1.6! . 8x3 = 84.8x3= 672x3. Portanto o sétimo termo procurado é 672x3.
3) Determine o termo independente de x no desenvolvimento de (x + 1/x )6 .
Solução:
Sabemos que o termo independente de x é aquele que não depende de x, ou seja, aquele que não possui x.
Temos no problema dado: a = x , b = 1/x e n = 6.
Pela fórmula do termo geral, podemos escrever:
Temos no problema dado: a = x , b = 1/x e n = 6.
Pela fórmula do termo geral, podemos escrever:
Tp+1 = C6,p . x6-p . (1/x)p = C6,p . x6-p . x-p = C6,p . x6-2p .
Ora, para que o termo seja independente de x, o expoente desta variável deve ser zero, pois x0 = 1. Logo, fazendo 6 - 2p = 0, obtemos p=3. Substituindo então p por 6, teremos o termo procurado. Temos então:
T3+1 = T4 = C6,3 . x0 = C6,3 = 6! /[(6-3)! . 3! ] = 6.5.4.3! / 3!.3.2.1 = 20.
Logo, o termo independente de x é o T4 (quarto termo) que é igual a 20.
Ora, para que o termo seja independente de x, o expoente desta variável deve ser zero, pois x0 = 1. Logo, fazendo 6 - 2p = 0, obtemos p=3. Substituindo então p por 6, teremos o termo procurado. Temos então:
T3+1 = T4 = C6,3 . x0 = C6,3 = 6! /[(6-3)! . 3! ] = 6.5.4.3! / 3!.3.2.1 = 20.
Logo, o termo independente de x é o T4 (quarto termo) que é igual a 20.
4) O binômio de Newton foi desenvolvido para facilitar as adições e subtrações de termos algébricos elevados a expoentes maiores que 3. Com base nas técnicas apresentadas pelo binômio, calcule o desenvolvimento da expressão  .
.
 .
.
Solução:

5) Utilizando o desenvolvimento do binômio de Newton, calcule o desenvolvimento da expressão (2x + 1)4.
Solução:

No desenvolvimento de (3x + 13)n há 13 termos. A soma dos coeficientes destes termos
é igual a:
é igual a:
Resp;248
6) UF. VIÇOSA - A soma dos coeficientes do desenvolvimento de (2x + 3y)m é 625. O valor de m é:
a) 5
b) 6
c)10
d) 3
e) 4
a) 5
b) 6
c)10
d) 3
e) 4
7) Calcule a soma dos coeficientes do desenvolvimento do binômio (3x - 1)10.
Resp: 1024
Resp: 1024
8) (CESGRANRIO) O coeficiente de x4 no polinômio P(x) = (x + 2)6 é:
a) 64
b) 60
c) 12
d) 4
e) 24
9) (UNESP) Se n é um número inteiro positivo, pelo símbolo n! subentende-se o produto de n fatores distintos, n . (n - 1) . (n - 2) ... 2 . 1. Nestas condições, qual é o algarismo das unidades do número (9!8!)7!?
a) 0
b) 1
c) 2
d) 3
e) 4
10) Se um dos termos do desenvolvimento do binômio (x + a)¦, com a  IR, é 80x², então o valor de a é
IR, é 80x², então o valor de a é
a) 6
b) 5
c) 4
d) 3
e) 2
b) 5
c) 4
d) 3
e) 2
11) No desenvolvimento de (x + y)n, a diferença entre os coeficientes do 3(0). e do 2(0). termos é igual a 54. Podemos afirmar que o termo médio é o:
a) 3(0).
b) 4(0).
c) 5(0).
d) 6(0).
e) 7(0).
12) Se a soma dos coeficientes do desenvolvimento do binômio (2x + y)n é igual a 243, então o número n é
b) 4(0).
c) 5(0).
d) 6(0).
e) 7(0).
12) Se a soma dos coeficientes do desenvolvimento do binômio (2x + y)n é igual a 243, então o número n é
a) 12
b) 10
c) 8
d) 5e) 3
b) 10
c) 8
d) 5e) 3
13) A expressão n! 3n+1/[3n² (n + 2) !] é equivalente a:
a) 27/(n² + 3n + 2)b) (n - 1)/(9n + 18)
c) n + 1
d) 27n² + 81n + 54
e) 27n + 54
c) n + 1
d) 27n² + 81n + 54
e) 27n + 54
14) No desenvolvimento do binômio [4vx + (1/vx)]1(0), segundo as potências decrescentes de x, o sétimo termo é:


Resp: C
15) Calcule o valor da expressão a seguir (imagem abaixo) , onde n é ímpar, justificando a sua resposta.

Resposta: Zero, pois os termos binomiais equidistantes dos extremos são complementares e, portanto, iguais, e possuem sinais contrários, anulando-se dois a dois.
16) (UFPR) Considerando o Binômio [x² + (1/x)]n, assinale o que for correto.
01) Se n é um número par, o desenvolvimento desse Binômio tem um número ímpar de termos.
02) Se a soma dos coeficientes do desenvolvimento desse Binômio é 256, então (n/2)!=24
04) Se o desenvolvimento desse Binômio possui seis termos, a soma de seus coeficientes é 32
08) Se n = 4, o termo médio desse Binômio é independente de x
16) O produto do primeiro termo do desenvolvimento desse Binômio pelo seu último termo é xn, para qualquer valor de n N*
N*
01) Se n é um número par, o desenvolvimento desse Binômio tem um número ímpar de termos.
02) Se a soma dos coeficientes do desenvolvimento desse Binômio é 256, então (n/2)!=24
04) Se o desenvolvimento desse Binômio possui seis termos, a soma de seus coeficientes é 32
08) Se n = 4, o termo médio desse Binômio é independente de x
16) O produto do primeiro termo do desenvolvimento desse Binômio pelo seu último termo é xn, para qualquer valor de n
Resp: 23
17) Se a e b são números reais tais que (a + b)1(0) = 1024 e se o 6(0). termo do desenvolvimento binomial é igual a 252, então:
a) a = 1/2 e b = 3/2
b) a = 3 e b = -1
c) a = 2/3 e b = 4/3
d) a = 1/3 e b = 5/3
e) a = 1 e b = 1
b) a = 3 e b = -1
c) a = 2/3 e b = 4/3
d) a = 1/3 e b = 5/3
e) a = 1 e b = 1
Sabendo que:
x e y são números positivos
x - y = 1 e
x4 + 4x³y + 6x²y² + 4xy³ + y4 = 16
podemos concluir que:
x e y são números positivos
x - y = 1 e
x4 + 4x³y + 6x²y² + 4xy³ + y4 = 16
podemos concluir que:
a) x = 7/6
b) x = 6/5
c) x = 5/4
d) x = 4/3
e) x = 3/2
b) x = 6/5
c) x = 5/4
d) x = 4/3
e) x = 3/2
18) No triângulo de Pascal
n = 0 1
n = 1 1 1
n = 2 1 2 1
n = 3 1 3 3 1
n = 4 1 4 6 4 1
. . . . . . . . .
a soma dos elementos da linha n com os da linha n + 1 é
a) n ( n + 1 )
b) 2n . 2n+1
c) 3 . 2n
d) 2 . 2n+1
e) 3n . 2n+1
19) Desenvolvendo o binômio (2x - 1)8, o quociente entre o quarto e o terceiro termos é
a) - 4
b) - x
c) x
d) - 1/xe) 4x
b) - x
c) x
d) - 1/xe) 4x
20) Para que o termo médio do desenvolvimento do binômio (sen x + cos x)6, segundo as potências decrescentes de sen x, seja igual a 5/2, o arco x deve ter sua extremidade pertencente ao
a) primeiro ou segundo quadrantes.
b) primeiro ou terceiro quadrantes.c) segundo ou terceiro quadrantes.
d) eixo das abscissas.
e) eixo das ordenadas.
b) primeiro ou terceiro quadrantes.c) segundo ou terceiro quadrantes.
d) eixo das abscissas.
e) eixo das ordenadas.


Nenhum comentário:
Postar um comentário