Triângulo - conceito
Do latim - triangulu, é um polígono de três lados e três ângulos. Os três ângulos de um triângulo são designados por três letras maiúsculas A, B e C e os lados opostos a eles, pelas mesmas três letras, minúsculas a, b e c.
Do latim - triangulu, é um polígono de três lados e três ângulos. Os três ângulos de um triângulo são designados por três letras maiúsculas A, B e C e os lados opostos a eles, pelas mesmas três letras, minúsculas a, b e c.

Classificação dos triângulos
Os triângulos classificam-se...
Quanto aos lados | ||
 |  | |
3 lados iguais
é o
Triângulo
Equilátero
|
2 lados iguais
e 1 diferente é oTriângulo
Isósceles
|
3 lados diferentes
é o
Triângulo
Escaleno
|
Quanto aos ângulos
| ||
 |  | |
3 ângulos agudos
é o
Triângulo
acutângulo |
1ângulo reto
é o
Triângulo
rectângulo |
1 ângulo obtuso
é o
Triângulo obtusângulo
|
Elementos do triângulo
| |||||||||||||||||||||||||||||||||||||
O triângulo é um polígono com três lados. Os três pontos não colineares são os vértices do triângulo: A, B e C.
| |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
Como se relacionam os lados e os ângulos de um triângulo?
| ||||
| ||||
Sabia-se que
Assim, aos dois ângulos iguais opõem-se os dois lados iguais.
De um modo geral:
|  | |||
Num triângulo, a ângulos iguais opõem-se lados iguais e a lados iguais opõem-se ângulos iguais.
| ||||
Critérios de igualdade de triângulos
| ||||||||||||||
Caso I
|
Caso II
|
Caso III
| ||||||||||||
|
|
| ||||||||||||
Pontos notáveis do triângulo
O Circuncentro
| ||
A mediatriz do lado de um triângulo é uma recta perpendicular ao lado no seu ponto Médio. Se traçarmos as mediatrizes dos três lados de um triângulo, elas intersectam-se num ponto O, chamado circuncentro. Este ponto está equidistante (à mesma distância) dos três vértices do triângulo e é o centro duma circunferência circunscrita ao mesmo. | ||
 | ||
O Incentro
| ||
A bissetriz de um ângulo interno de um triângulo é a semi-reta interior do ângulo que o divide em dois ângulos geometricamente iguais.
As bissetrizes dos ângulos internos dum triângulo intersectam-se num ponto chamado incentro I, que está à mesma distância (equidistante) dos lados do mencionado triângulo e é o centro de uma circunferência inscrita no mesmo.
| ||
 | ||
O Ortocentro
| ||
A altura de um triângulo é o segmento perpendicular compreendido entre o vértice e o lado oposto.
Um triângulo admite três alturas.
As alturas (Ha,Hb e Hc) de um triângulo intersectam-se num ponto H,chamado ortocentro.
| ||
 | ||
Baricentro de um triângulo
Considere o triângulo de vértices A, B e C abaixo. Os pontos M, N e P são os pontos médios dos lados AB, BC e AC, respectivamente. Os segmentos de reta MC, AN e PB são as medianas do triângulo. Denominamos baricentro (G) de um triângulo o ponto de encontro das medianas.
Agora vamos considerar um triângulo no plano cartesiano de vértices A(xA, yA), B(xB, yB) e C(xC, yC) e baricentro G(xG, yG).
As coordenadas do baricentro do triângulo ABC serão dadas por:

Exemplo 1. Determine as coordenadas do baricentro do triângulo de vértices A(2, 7), B(5, 3) e C(2, 2).
Solução: Vamos calcular as coordenadas do Baricentro do triângulo separadamente, para não haver confusão no entendimento da fórmula, que é muito simples.
Sabemos que:
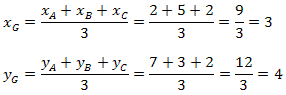
Portanto, o baricentro do triângulo ABC tem coordenadas G(3, 4).
Exemplo 2. Determine as coordenadas do vértice B do triângulo ABC sabendo que seu baricentro tem coordenadas G(5, 8) e que os outros dois vértices são A(5, 8) e C(7, 6).
Solução: Como conhecemos as coordenadas do baricentro do triângulo e as coordenadas de dois vértices, vamos utilizar a fórmula para a determinação do baricentro para determinar as coordenadas de B.
Segue que:
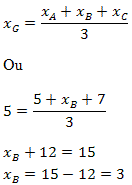
Temos também que:

Portanto, o vértice B tem coordenadas B(3, 10).

Exemplo 1. Determine as coordenadas do baricentro do triângulo de vértices A(2, 7), B(5, 3) e C(2, 2).
Solução: Vamos calcular as coordenadas do Baricentro do triângulo separadamente, para não haver confusão no entendimento da fórmula, que é muito simples.
Sabemos que:
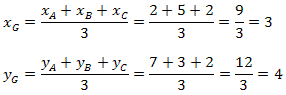
Portanto, o baricentro do triângulo ABC tem coordenadas G(3, 4).
Exemplo 2. Determine as coordenadas do vértice B do triângulo ABC sabendo que seu baricentro tem coordenadas G(5, 8) e que os outros dois vértices são A(5, 8) e C(7, 6).
Solução: Como conhecemos as coordenadas do baricentro do triângulo e as coordenadas de dois vértices, vamos utilizar a fórmula para a determinação do baricentro para determinar as coordenadas de B.
Segue que:
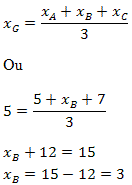
Temos também que:

Portanto, o vértice B tem coordenadas B(3, 10).
Semelhança e congruência de triângulos
Temos que dois triângulos são congruentes:
Quando seus elementos (lados e ângulos) determinam a congruência entre os triângulos.
Quando dois triângulos determinam a congruência entre seus elementos.
Casos de congruência:
1º LAL (lado, ângulo, lado): dois lados congruentes e ângulos formados também congruentes.

2º LLL (lado, lado, lado): três lados congruentes.
Quando seus elementos (lados e ângulos) determinam a congruência entre os triângulos.
Quando dois triângulos determinam a congruência entre seus elementos.
Casos de congruência:
1º LAL (lado, ângulo, lado): dois lados congruentes e ângulos formados também congruentes.

2º LLL (lado, lado, lado): três lados congruentes.

3º ALA (ângulo, lado, ângulo): dois ângulos congruentes e lado entre os ângulos congruente.

4º LAA (lado, ângulo, ângulo): congruência do ângulo adjacente ao lado, e congruência do ângulo oposto ao lado.
.jpg)
Através das definições de congruência de triângulos podemos chegar às propriedades geométricas sem a necessidade de efetuar medidas. A esse método damos o nome de demonstração.
Dizemos que, em todo triângulo isósceles, os ângulos opostos aos lados congruentes são congruentes. Os ângulos da base de um triângulo isósceles são congruentes.
Componentes do triângulo retângulo
No estudo da geometria plana e da trigonometria, um dos protagonistas é o triângulo retângulo, pois dele obtemos algumas teorias como Teorema de Pitágoras, relações trigonométricas etc. Mas para que possamos compreender todas essas teorias, primeiramente faz-se necessário entender a composição do triângulo retângulo.
Inicialmente, ele recebe essa classificação de retângulo, pois um de seus ângulos é reto (90°), como podemos constatar na imagem a seguir.
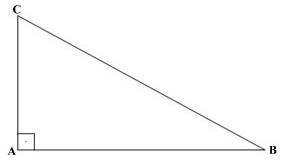
Com isso, resta-nos entender a característica dos outros dois ângulos deste triângulo, para isso façamos a seguinte reflexão: A soma dos ângulos internos de um triângulo é 180°, um destes ângulos nós conhecemos, que é o ângulo reto, então a soma dos outros dois ângulos deverá ser 90°.
Do raciocínio anterior, podemos concluir que os outros dois ângulos deverão ser ângulos agudos.
Agora veremos os elementos não menos importantes neste triângulo, que constitui a relação de proporção entre cada ângulo e o lado oposto a este ângulo. No caso do triângulo retângulo, nomeamos os lados de duas maneiras: catetos e hipotenusa.
Dentre os catetos, teremos uma divisão entre: cateto oposto e cateto adjacente, e veremos que para cada ângulo que tomarmos como referência, cada cateto receberá uma classificação em especial.
Mas, e a hipotenusa? A hipotenusa sempre será o lado oposto ao ângulo reto, no caso da Figura 1, a hipotenusa é o segmento de reta AB.
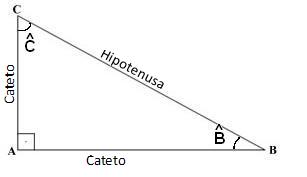
Vamos classificar os catetos deste ângulo: Temos dois catetos (os segmentos AC e BC) que receberão classificação de cateto oposto e cateto adjacente, dependendo do ângulo que tomamos como referência.

Sendo assim, podemos falar que:
Cateto Oposto: é o lado oposto ao ângulo que se observa.
Cateto Adjacente: é o lado vizinho ao ângulo que se observa.
Exercícios resolvidos e propostos sobre semelhança e congruência de triângulos
1) Um triângulo ABC tem os lados AB = 12m, AC = 13m e BC = 15m. A reta paralela ao lado BC do triângulo determina um triângulo ADE, em que DE = 5cm. Calcular AD e AE.
Resolução


AB = 12
AC = 13
BC = 15
DE = 5
Calcular
AD = x
AE = y



Resposta: AD = 4m e AE = m
m
Resolução


AB = 12
AC = 13
BC = 15
DE = 5
Calcular
AD = x
AE = y



Resposta: AD = 4m e AE =
 m
m
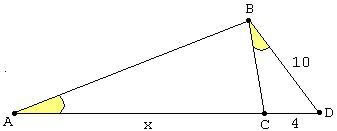
2) Determine a medida x na figura abaixo:
Solução:
Observe que os triângulos ABD e CBD são semelhantes, pois possuem dois ângulos de mesma medida: o ângulo comum D e aqueles marcados em amarelo. Separando os triângulos, vem:
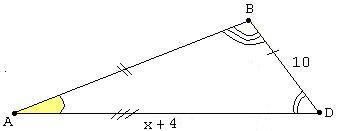
Comparando os lados correspondentes marcados nas duas figuras acima, vem imediatamente que:
BD / CD = AD / BD = AB / BC
Substituindo os valores, vem:
10 / 4 = (x + 4) / 10
Resolvendo a equação acima, fica:
4(x + 4) = 10.10
x + 4 = 100/4
x + 4 = 25 \ x = 21
Resp: x = 21

Solução:
Observe que os triângulos ABD e CBD são semelhantes, pois possuem dois ângulos de mesma medida: o ângulo comum D e aqueles marcados em amarelo. Separando os triângulos, vem:


Comparando os lados correspondentes marcados nas duas figuras acima, vem imediatamente que:
BD / CD = AD / BD = AB / BC
Substituindo os valores, vem:
10 / 4 = (x + 4) / 10
Resolvendo a equação acima, fica:
4(x + 4) = 10.10
x + 4 = 100/4
x + 4 = 25 \ x = 21
Resp: x = 21
3) Dados os triângulos semelhantes PTN e AMO, semelhantes

com AM = 3 cm, MO = 7 cm e AO = 5 cm, pede-se calcular a razão de semelhança e os outros dois lados do
 , sabendo-se que PT = 6cm.
, sabendo-se que PT = 6cm.
Resolução

Como sabemos:
A razão de semelhança é 2
Resposta: A razão de semelhança é 2 e os outros dois lados do
 medem 10 cm e 14 cm.
medem 10 cm e 14 cm.No  ABC da figura, sabemos que AB = 10 cm, BC = 8cm, AC = 14 cm, AS = 5 cm e ABC da figura, sabemos que AB = 10 cm, BC = 8cm, AC = 14 cm, AS = 5 cm e  . Calcular RS e AR. . Calcular RS e AR.
Resolução
Devemos perceber que o ângulo A é comum aos dois triângulos. Separamos os triângulos para visualizar melhor o caso de semelhança. 
Vamos aplicar o caso AA:
Resposta: RS = 4 e AR = 7. |
a)
x + 70o + 60o = 180o
x = 180o - 130o
x = 50o
b)
Devemos escolher um dos segmentos apontados na figura para prolongar, a fim de encontrarmos dois triângulos:
A partir dos valores que já temos, vamos achar o valor de x:
6) Dado os triângulos retângulos ARE e OTE:


Responder Verdadeiro ou Falso nas questões 8 a 11.
8) Num triângulo isósceles, o circuncentro coincide com o baricentro. ( )
9) Se o ortocentro é vértice o triângulo é retângulo. ( )
14) Assinale V ou F
15) Encontre o valor de x no triângulo abaixo:

16) Encontre o valor de x, y e z no triângulo abaixo:
.jpg)
Gabarito:
 |
x + 70o + 60o = 180o
x = 180o - 130o
x = 50o
b)
 |
Devemos escolher um dos segmentos apontados na figura para prolongar, a fim de encontrarmos dois triângulos:
 |
 |
A partir dos valores que já temos, vamos achar o valor de x:
 |
6) Dado os triângulos retângulos ARE e OTE:

Se AR = OE = 2 AE, então:
(A) OE < TO
(B) AE < ER
(C) OE = TO
(D) AE = ER
(E) AR + TE > OT
(A) OE < TO
(B) AE < ER
(C) OE = TO
(D) AE = ER
(E) AR + TE > OT
7) Dado os triângulos retângulos ARE e OTE:

Se OE = 10, TO = 8 e AE = 20, então:
(A) AR = 20
(B) AR = 24
(C) AR = 16
(D) AR = 14
(E) AR = 12
8) Num triângulo isósceles, o circuncentro coincide com o baricentro. ( )
9) Se o ortocentro é vértice o triângulo é retângulo. ( )
10) Se o circuncentro é externo, o triângulo é obtusângulo. ( )
11) Se o baricentro, o incentro, o circuncentro e o ortocentro estão alinhados, o triângulo é isósceles. ( )
12) (ENEM) Determine a medida do lado AB do triangulo ABC abaixo, sabendo que
BAC ≡ DBC.
a) 0,8 cm
b) 8 cm
c) 80 cm
d) 4 cm
e) 16 cm
13) (CEFET-RJ) Na figura, os segmentos BC e DE são paralelos, AB=15cm, AD=5cm e AE=6cm. A medida do segmento CE é, em centímetros:
a) 5 cm
b) 6 cm
c) 10 cm
d) 12 cm
e) 18 cm
a) Todo triângulo equilátero é também equiângulo. ( )
b) Todos os triângulos equiláteros são semelhantes. ( )
c) Todos os triângulos isósceles são semelhantes. ( )
d) Todos os losangos são semelhantes ( )
15) Encontre o valor de x no triângulo abaixo:

16) Encontre o valor de x, y e z no triângulo abaixo:
.jpg)
Gabarito:
6) E 7) C 8) Falso 9) Verdadeiro 10) Verdadeiro 11) Verdadeiro 12) B 13) D
14) a) V b) V c) F d) F 15) x = 70º 16) x = 105º, y = 60º e z = 15º
14) a) V b) V c) F d) F 15) x = 70º 16) x = 105º, y = 60º e z = 15º



















Muito boa a explicação e os exercícios muito bem reformulado, parabéns!
ResponderExcluir