SENTENÇAS
Uma sentença matemática pode ser verdadeira ou falsa
exemplo de uma sentença verdadeira
a) 15 + 10 = 25
b) 2 . 5 = 10
exemplo de uma sentença falsa
a) 10 + 3 = 18
b) 3 . 7 = 20
SENTENÇAS ABERTAS E SENTENÇAS FECHADAS
Sentenças abertas são aquelas que possuem elementos desconhecidos. Esses elementos desconhecidos são chamados variáveis ou incógnitas.
exemplos
a) x + 4 = 9 (a variável é x)
b) x + y = 20 (as variáveis são x e y)
Sentenças fechada ou são aquelas que não possuem variáveis ou incógnitas.
a) 15 -5 = 10 (verdadeira)
b) 8 + 1 = 12 (falsa)
EQUAÇÕES
Equações são sentenças matemáticas abertas que apresentam o sinal de igualdade
exemplos
a) x - 3 = 13 ( a variável ou incógnita x)
b) 3y + 7 = 15 ( A variável ou incógnita é y)
A expressão à esquerdas do sinal = chama-se 1º membro
A expressão à direita do sinal do igual = chama-se 2º membro
Incógnitas e coeficientes
Em tempos remotos os valores desconhecidos de um determinado problema eram nomeados pelos árabes de xay e em outros casos, até mesmo por outros povos, a sua referência era feita através de figuras geométricas. Em dias atuais a nomenclatura utilizada para determinar o que se quer encontrar em problemas matemáticos é incógnita. Esta palavra deriva do latim incognitu que também significa coisa desconhecida.
A letra a ser usada para representar o valor desconhecido fica a critério do autor da questão, o que realmente importa é a facilitação do cálculo de equações com a introdução dessa ferramenta algébrica aliada a aritmética, a geometria e tantos outros ramos da matemática. Sendo assim, pode-se, ao invés do x, usar-se a, b, c, d,… z, etc.
Em linguagem matemática, se temos uma expressão do tipo 2x – 4 = 0 destacam-se:
- 2 e 4 são coeficientes – representam respectivamente fator e subtraendo da equação exemplificada;
- x é incógnita – valor desconhecido ao qual se está buscando encontrar;
- para x = 2 temos uma sentença verdadeira, ou seja, 2 . 2 – 4 = 0. Ao valor que substituído pela incógnita torna a sentença verdadeira dá-se o nome de raiz da equação. Nesse caso o algarismo 2 é a raiz da equação 2x – 4 = 0.
Exemplos
- 4x + 16 = 0, 4 e 16 são coeficientes, x é incógnita;
- n – 2 = 0, 1 e -2 são coeficientes (o desprezo do 1 não altera o equilíbrio da equação uma vez 1.n =n) e n é a incógnita;
- 1/3a – 5/3 = 0, 1/3 e 5/3 são coeficientes, a é a incógnita.
RESOLUÇÃO DE EQUAÇÕES DO 1º GRAU COM UMA VARIÁVEL
O processo de resolução está baseado nas propriedades das igualdades
1º Propriedade
Podemos somar (ou subtrair) um mesmo número dos dois membros da igualdade, obtendo uma sentença equivalente.
exemplos:
a) Resolver x - 3 = 5
solução
x - 3 +3 = 5 + 3
x + 0 = 8
x = 8
b) resolver x + 2 = 7
solução
x+2 -2 = 7 - 2
x + 0 = 5
x = 5
Baseado nessa propriedade,podemos concluir que: pode-se passar um termo de um membro para outro e troca-se o sinal desse termo.
exemplos
a) x - 3 = 5
x = x + 3
x = 8
b) x + 2 = 7
x = 7 - 2
x = 5
2ª Propriedade
Podemos multiplicar (ou dividir) ambos os membros de uma igualdade por um número diferentes de zero, obtendo uma sentença equivalente.
Exemplo de resolução pelo modo prático
a) 3x =12
x = 12 /3
x = 4
b) x / 5 = 2
x = 2 . 5
x = 10
Importante !
Veja a equação -x = 5
interessa-nos valor de x e não o valor de -x então devemos multiplicar os dois membros da equação por -1
REGRA PRÁTICA PARA RESOLUÇÃO DE EQUAÇÕES DO 1º GRAU
Para resolver equação de 1° grau usaremos um método pratico seguindo o roteiro:
1) Isolar no 1° membro os termos em x e no 2° membro os termos que não apresentam x ( devemos trocar o sinal dos termos que mudam de membro para outro)
2) Reduzir os termos semelhantes
3) Dividir ambos os membros pelo coeficiente de x
Exemplos:
1) 4X – 4 = 2X + 8
4X- 2X = 8 + 4
2X = 12
X = 12/2
X = 6
2) 9X – 2 + 4 = 10 + 7X
9X – 7X = 10 + 2 – 4
9X – 7X = 10 + 2 – 4
2X = 8
X = 8/2
X= 4
3) 5(X + 2) =1
5X + 10 = 1
5X = 1 – 10
X = -9/5
4) 5(2x - 4) = 7 ( x + 1) – 3
10x – 20 = 7x + 7 -3
10x – 7x = 7 -3 + 20
3x = 24
x = 24/ 3
x = 8
5) x/3 + x/2 = 15
2x / 6 + 3x / 6 = 90 / 6
2x + 3x = 90
5x = 90
x = 90 / 5
x = 18
Equações de primeiro grau com duas variáveis
Considere a equação: 2x - 6 = 5 - 3y
Trata-se de uma equação com duas variáveis, x e y, pode ser transformada numa equação equivalente mais simples. Assim:
2x + 3y = 5 + 6
2x + 3y = 11 ==> Equação do 1º grau na forma ax + by = c .
| Denominando equação de 1º grau com duas variáveis, x e y, a toda equação que pode ser reproduzida à forma ax + by = c, sendo a e b números diferentes de zero, simultaneamente. |
Na equação ax + by = c, denominamos:
| x + y - variáveis ou incógnita a - coeficiente de x | b - coeficiente de y c - termo independente |
Exemplos:
| x + y = 302x + 3y = 15 x - 4y = 10 | -3x - 7y = -482x- 3y = 0 x - y = 8 |
Solução de uma equação de 1º grau com duas variáveis
Quais o valores de x e y que tornam a sentença x - 2y = 4 verdadeira?
Observe os pares abaixo:
x = 6, y = 1
x - 2y = 4
6 - 2 . 1 = 4
6 - 2 = 4
4 = 4 (V)
|
x = 8, y = 2
x - 2y = 4
8 - 2 . 2 = 4
8 - 4 = 4
4 = 4 (V)
|
x = -2, y = -3
x - 2y = 4
-2 - 2 . (-3) = 4
-2 + 6 = 4
4 = 4 (V)
|
Verificamos que todos esses pares são soluções da equação x - 2y = 4.
Assim, os pares (6, 1); (8, 2); (-2, -3) são algumas das soluções dessa equação.
Uma equações do 1º grau com duas variáveis tem infinitas soluções - infinitos (x, y) - , sendo, portanto, seu conjunto universo 
.
.
Podemos determinar essas soluções, atribuindo-se valores quaisquer para uma das variáveis, calculando a seguir o valor da outra. Exemplo:
- Determine uma solução para a equação 4x - 3y = 11.
Atribuímos para x o valor 2, e calculamos o valor de y. Assim:
x = 2
4 * 2 – 3y = 11
8 – 3y = 11
– 3y = 11 – 8
– 3y = 3 (multiplicar por – 1)
3y = – 3
y = – 3/3
y = – 1
Estabelecendo x = 2, temos y = – 1, constituindo o par ordenado (2, –1).
4 * 2 – 3y = 11
8 – 3y = 11
– 3y = 11 – 8
– 3y = 3 (multiplicar por – 1)
3y = – 3
y = – 3/3
y = – 1
Estabelecendo x = 2, temos y = – 1, constituindo o par ordenado (2, –1).
Resumindo:
| Um par ordenado (r, s) é solução de uma equação ax + by = c (a e b não-nulos simultaneamente), se para x = r e y = s a sentença é verdadeira. |
Exemplo 2
Dada a equação x – 4y = –15, determine os pares ordenados obedecendo ao intervalo numérico –3 ≤ x ≤ 3.
x = –3
–3 – 4y = – 15
– 4y = –15 + 3
– 4y = – 12
4y = 12
y = 3
x = – 2
–2 – 4y = – 15
– 4y = –15 + 2
– 4y = – 13
4y = 13
y = 13/4
x = – 1
–1 – 4y = – 15
– 4y = –15 + 1
– 4y = – 14
4y = 14
y = 14/4 = 7/2
x = 0
0 – 4y = – 15
– 4y = – 15
4y = 15
y = 15/4
x = 1
1 – 4y = – 15
– 4y = – 15 – 1
– 4y = – 16
4y = 16
y = 4
x = 2
2 – 4y = – 15
– 4y = – 15 – 2
– 4y = – 17
4y = 17
y = 17/4
x = 3
3 – 4y = – 15
– 4y = – 15 – 3
– 4y = – 18
4y = 18
y = 18/4 = 9/2
.jpg)
1) Resolva as seguintes equações
a) 3x = 15 (R=5)
b) 2x = 14 ( R=7)
c) 4x = -12 (R=-3)
d) 7x = -21 (R=-3)
e) 13x = 13 (R= 1)
f) 9x = -9 (R=-1)
g) 25x = 0 (R=0)
h) 35x = -105 (R=-3)
i) 4x = 1 (R=1/4)
j) 21 = 3x (R=7)
l) 84 = 6x (R=14)
m) x/3 =7 (R=21)
n) x/4 = -3 (R=-12)
o) 2x/5 = 4 (R=10)
p) 2x/3 = -10 (R=-15)
q) 3x/4 = 30 (R=40)
r) 2x/5 = -18 (R= -45)
s) x + 10 = 6x (R= 2)
t) x + 28 = 11 (R=-17)
u) x - 109 = 5 (R= 114)
v) x - 39 = -79 (R=-40)
x) 10x = x + 9 (R=1)
z) 2x = x + 20 (R= 20)
2) 7 é raiz da equação x + 2 = 4?
3) Encontre o conjunto verdade da equação 6x = -20 + 4x?
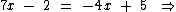
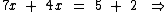
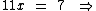
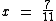
Chamamos problemas do 1º grau aqueles que são resolvidos por meio de uma equação do 1º grau.
Na resolução de problemas, você deve:
a) Representar a incógnita do problema por uma letra.
b) Armar a equação do problema.
c) Resolver a equação
d) verificar se a solução satisfaz as condições do problema.
Exemplo 1
O triplo de um número, diminuído de 12 é igual a 33. Qual é esse número
solução:
Triplo de um número === 3x
Diminuido de 12 ======3x -12
é igual a 33 =========3x - 12 = 33
Resolução
3x - 12 = 33
3x = 33 + 12
3x = 45
x = 45 / 3
x = 15
Resposta: O número procurado é 15
Exemplo 2
Um número somado com o seu dobro é igual a 21. Qual é esse número
Solução:
Um número -----------------------x
Somado com seu dobro--------- x + 2x
é igual a 21 -----------------------x + 2x = 21
Resolução:
x + 2x = 21
3x = 21
x = 21 / 3
x = 7
Resposta: O número procurado é 7.
http://www.mundovestibular.com.br/articles/57/1/EQUACOES-DO-PRIMEIRO-GRAU/Paacutegina1.html
Dada a equação x – 4y = –15, determine os pares ordenados obedecendo ao intervalo numérico –3 ≤ x ≤ 3.
x = –3
–3 – 4y = – 15
– 4y = –15 + 3
– 4y = – 12
4y = 12
y = 3
x = – 2
–2 – 4y = – 15
– 4y = –15 + 2
– 4y = – 13
4y = 13
y = 13/4
x = – 1
–1 – 4y = – 15
– 4y = –15 + 1
– 4y = – 14
4y = 14
y = 14/4 = 7/2
x = 0
0 – 4y = – 15
– 4y = – 15
4y = 15
y = 15/4
x = 1
1 – 4y = – 15
– 4y = – 15 – 1
– 4y = – 16
4y = 16
y = 4
x = 2
2 – 4y = – 15
– 4y = – 15 – 2
– 4y = – 17
4y = 17
y = 17/4
x = 3
3 – 4y = – 15
– 4y = – 15 – 3
– 4y = – 18
4y = 18
y = 18/4 = 9/2
Questões resolvidas sobre equação do 1º grau
1) Resolva as seguintes equações
a) 3x = 15 (R=5)
b) 2x = 14 ( R=7)
c) 4x = -12 (R=-3)
d) 7x = -21 (R=-3)
e) 13x = 13 (R= 1)
f) 9x = -9 (R=-1)
g) 25x = 0 (R=0)
h) 35x = -105 (R=-3)
i) 4x = 1 (R=1/4)
j) 21 = 3x (R=7)
l) 84 = 6x (R=14)
m) x/3 =7 (R=21)
n) x/4 = -3 (R=-12)
o) 2x/5 = 4 (R=10)
p) 2x/3 = -10 (R=-15)
q) 3x/4 = 30 (R=40)
r) 2x/5 = -18 (R= -45)
s) x + 10 = 6x (R= 2)
t) x + 28 = 11 (R=-17)
u) x - 109 = 5 (R= 114)
v) x - 39 = -79 (R=-40)
x) 10x = x + 9 (R=1)
z) 2x = x + 20 (R= 20)
2) 7 é raiz da equação x + 2 = 4?
x + 2 = 4
x = 4 - 2
x = 2
3) Encontre o conjunto verdade da equação 6x = -20 + 4x?
6x - 4x = - 20
2x = - 20
x = -20/2
x = - 10
4) Qual é a raiz da equação 7x - 2 = -4x + 5?
Portanto:
7/11 é a raiz da equação.
5) Nos itens que se seguem, determine duas soluções distintas para as equações:
Resolução:
5) Nos itens que se seguem, determine duas soluções distintas para as equações:
a) 5x-2y=9
b)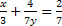 
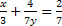
Resolução:
a) Vamos supor que x=0, substituindo na equação temos 5*0-2y=9, que é equivalente a -2y=9. Então, basta isolar a variável y, assim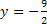 
. Logo, uma solução é o par 
.
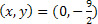Agora, para encontrar outra solução, podemos supor y=0, após substituirmos na equação original temos 5x=9. Isolando a variável x, temos que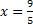
. Portanto, outra solução seria o par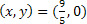 
b) Vamos supor que x=0, substituindo na equação temos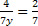
. Então basta isolar a variável y, assim 
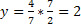. Logo, uma solução é o par (x,y)=(0,2).
Agora, para encontrar outra solução, não podemos supor y=0, pois assim o denominador da segunda parcela seria zero, e não existe divisão por zero. Assim, vamos supor y=1, após substituirmos na equação original, temos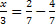
. Isolando a variável x e fazendo a subtração, temos que 
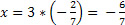. Portanto, outra solução seria o par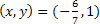 
6) Escreva duas equações distintas de 1º grau com duas incógnitas que apresentem como solução o ponto (3,4).
Resolução:
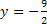. Logo, uma solução é o par 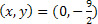.Agora, para encontrar outra solução, podemos supor y=0, após substituirmos na equação original temos 5x=9. Isolando a variável x, temos que
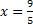. Portanto, outra solução seria o par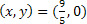 b) Vamos supor que x=0, substituindo na equação temos
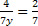. Então basta isolar a variável y, assim 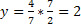. Logo, uma solução é o par (x,y)=(0,2).Agora, para encontrar outra solução, não podemos supor y=0, pois assim o denominador da segunda parcela seria zero, e não existe divisão por zero. Assim, vamos supor y=1, após substituirmos na equação original, temos
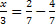. Isolando a variável x e fazendo a subtração, temos que 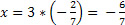. Portanto, outra solução seria o par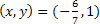 6) Escreva duas equações distintas de 1º grau com duas incógnitas que apresentem como solução o ponto (3,4).
Resolução:
Para encontrar duas equações que tenha como solução o ponto (x,y)=(3,4), podemos operar x e y de diversas formas, por exemplo, somar as variáveis, assim temos x+y=3+4=7, então a primeira equação pode ser x+y=7. E para encontrar a segunda equação, podemos dobrar o valor de x e subtrair do triplo de y, assim temos 2x-3y=2*3-3*4=6-12=-6 e a segunda equação seria 2x-3y=-6. Note que podemos obter infinitas soluções seguindo esse raciocínio.
7) Resolva as equações abaixo em R.
3x x - 10 x + 1
a) ——— - ——— = ————
2 8 4
Resolução:
. 8(3x) 2(x - 10) 4(x + 1) ——— - ——— = ———— 16 16 16 . 8(3x) -2(x - 10) = 4(x + 1) . 24x - 2x + 20= 4x + 4 . 24x - 2x - 4x = 4- 20 . 18x = - 16 . x = - 16/18 . x = - 8/ 9 . S = {-8/9} x + 6 2x - 3 x - 1 b) ——— - ——— = ———— 3 6 4 . 4(x + 6) 2(2x - 3) 3(x - 1) ————— - ————— = ———— 12 12 12
Resolução: . 4(x + 6) - 2(2x - 3) = 3(x - 1) . 4x + 24 - 4x + 6 = 3x - 3 . 4x - 4x - 3x = - 3 - 24 - 6 . - 3x = - 33 . 3x = 33 . x = 33/3 . x = 11 . S = {11}
8) (CFT-2005) Dois números reais x e y são tais que 
e 
.Sabendo que x 
-2 e y 
-3, o valor de “y – x” é
7) Resolva as equações abaixo em R.
Resolução:
. 8(3x) 2(x - 10) 4(x + 1) ——— - ——— = ———— 16 16 16 . 8(3x) -2(x - 10) = 4(x + 1) . 24x - 2x + 20= 4x + 4 . 24x - 2x - 4x = 4- 20 . 18x = - 16 . x = - 16/18 . x = - 8/ 9 . S = {-8/9} x + 6 2x - 3 x - 1 b) ——— - ——— = ———— 3 6 4 . 4(x + 6) 2(2x - 3) 3(x - 1) ————— - ————— = ———— 12 12 12
Resolução: . 4(x + 6) - 2(2x - 3) = 3(x - 1) . 4x + 24 - 4x + 6 = 3x - 3 . 4x - 4x - 3x = - 3 - 24 - 6 . - 3x = - 33 . 3x = 33 . x = 33/3 . x = 11 . S = {11}
e .Sabendo que x -2 e y -3, o valor de “y – x” é
a) 1.b) 2.
c) 3.
d) 4.
c) 3.
d) 4.
Problemas do 1º grau: aprenda com resolver
Na resolução de problemas, você deve:
a) Representar a incógnita do problema por uma letra.
b) Armar a equação do problema.
c) Resolver a equação
d) verificar se a solução satisfaz as condições do problema.
Exemplo 1
O triplo de um número, diminuído de 12 é igual a 33. Qual é esse número
solução:
Triplo de um número === 3x
Diminuido de 12 ======3x -12
é igual a 33 =========3x - 12 = 33
Resolução
3x - 12 = 33
3x = 33 + 12
3x = 45
x = 45 / 3
x = 15
Resposta: O número procurado é 15
Exemplo 2
Um número somado com o seu dobro é igual a 21. Qual é esse número
Solução:
Um número -----------------------x
Somado com seu dobro--------- x + 2x
é igual a 21 -----------------------x + 2x = 21
Resolução:
x + 2x = 21
3x = 21
x = 21 / 3
x = 7
Resposta: O número procurado é 7.
Gráfico de uma equação de 1º grau com duas variáveis
Sabemos que uma equação do 1º grau com duas variáveis possui infinitas soluções.
Cada uma dessas soluções pode ser representada por um par ordenado (x, y).
Dispondo de dois pares ordenados de um equação, podemos representá-los graficamente num plano cartesiano, determinando, através da reta que os une, o conjunto das solução dessa equação. Exemplo:
Construir um gráfico da equação x + y = 4.
Inicialmente, escolhemos dois pares ordenados que solucionam essa equação.
1º par: A (4, 0)
2º par: B (0, 4)
A seguir, representamos esses pontos num plano cartesiano.
|  |
Finalmente, unimos os pontos A e B, determinando a reta r, que contém todos os pontos soluções da equação.
 |
A reta r é chamada reta suporte do gráfico da equação.
Fontes:
http://jmpmat22.blogspot.com.br/http://www.mundovestibular.com.br/articles/57/1/EQUACOES-DO-PRIMEIRO-GRAU/Paacutegina1.html
Exercícios resolvidos e propostos sobre problemas do 1º grau
1) O volume de chuvas na minha região foi de 30 ml nos dois últimos dias. Sabe-se que ontem choveu o dobro da quantidade que choveu hoje. Qual foi o volume de chuva de hoje?
Resolução:
Chamemos de v o volume da chuva hoje.
Do enunciando tiramos que 2v corresponde ao volume de chuva de ontem, assim como 30 é o volume total. Podemos então montar à seguinte equação:
Somando os termos do primeiro membro temos:
Passando o 3 para o outro lado, como divisor já que ele é um multiplicador:
Ao dividirmos:
Portanto:
O volume de chuva de hoje foi de 10 ml.
2) A soma da minha idade, com a idade de meu irmão que é 7 anos mais velho que eu dá 37 anos. Quantos anos eu tenho de idade?
Resolução:
Partamos do princípio que a minha idade seja igual a x. Como o meu irmão tem 7 anos a mais que eu, então ele tem x + 7 anos de idade. Como a soma das idades é de 37 anos, podemos escrever a seguinte sentença:
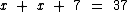
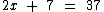
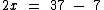
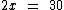
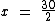
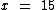
Resolução:
3p + 5 = 254 3p = 254 - 5 3p = 249 p = 249/3 p = 83
Resposta: Esse número é 83.
4) Um número mais a sua metade é igual a 150. Qual é esse número?
Resolução:
n + n/2 = 150 2n/2 + n/2 = 300/2 2n + n = 300 3n = 300 n = 300/3 n = 100
Resposta: Esse número é 100.
5) Em um concurso os participantes devem responder a um total de 20 questões. Para cada resposta correta o candidato ganha 3 pontos e para cada resposta errada perde 2 pontos. Determine o número de acertos e erros que um candidato obteve considerando que ele totalizou 35 pontos.
Resolução:
a) 4,0 m e 5,0 m.
b) 5,0 m e 6,0 m.
c) 6,0 m e 7,0 m.
d) 7,0 m e 8,0 m.
e) 8,0 m e 9,0 m.
Resolução:
Fazendo-se as considerações que:
- o alcance do segundo salto é 1,2 m menor que do primeiro salto
- o alcance do terceiro salto é 1,5 m menor que do segundo salto
- a distância alcançada no primeiro salto é x
Logo, para atingir a meta de 17,4 m, tem-se:
x + (x – 1,2) + (x – 1,2 – 1,5) = 17,4 ⇔3x = 21,3 ⇔ x = 7,1
Letra: D
Resolução:
Ou seja:
Passando para o outro lado o 7 como subtraindo, já que ele se encontra adicionando no primeiro membro, temos:
Realizando a subtração:
Passando o multiplicador 2 para a direita como divisor:
Que dividindo dá:
Portanto:
Eu tenho 15 anos de idade.
3) O triplo de um número, mais 5, é igual a 254. Qual é esse número?
Resolução:
3p + 5 = 254 3p = 254 - 5 3p = 249 p = 249/3 p = 83
Resposta: Esse número é 83.
4) Um número mais a sua metade é igual a 150. Qual é esse número?
Resolução:
n + n/2 = 150 2n/2 + n/2 = 300/2 2n + n = 300 3n = 300 n = 300/3 n = 100
Resposta: Esse número é 100.
5) Em um concurso os participantes devem responder a um total de 20 questões. Para cada resposta correta o candidato ganha 3 pontos e para cada resposta errada perde 2 pontos. Determine o número de acertos e erros que um candidato obteve considerando que ele totalizou 35 pontos.
Resolução:
Acertos: representados pela letra x.
Erros: representados por 20 − x.
Portanto:
3 * x – 2 * (20 – x) = 35
3x – 40 + 2x = 35
5x = 35 + 40
5x = 75
x = 75/5
x = 15
O candidato obteve 15 acertos e 5 erros.
Erros: representados por 20 − x.
Portanto:
3 * x – 2 * (20 – x) = 35
3x – 40 + 2x = 35
5x = 35 + 40
5x = 75
x = 75/5
x = 15
O candidato obteve 15 acertos e 5 erros.
6) (ENEM/2010) O Salto Triplo é uma modalidade do atletismo em que o atleta dá um salto em um só pé, uma passada e um salto, nessa ordem. Sendo que o salto com impulsão em um só pé será feito de modo que o atleta caia primeiro sobre o mesmo pé que deu a impulsão; na passada ele cairá com o outro pé, do qual o salto é realizado.
Disponível em: www.cbat.org.br (adaptado).
Um atleta da modalidade Salto Triplo, depois de estudar seus movimentos, percebeu que, do segundo para o primeiro salto, o alcance diminuía em 1,2 m, e, do terceiro para o segundo salto, o alcance diminuía 1,5 m. Querendo atingir a meta de 17,4 m nessa prova e considerando os seus estudos, a distância alcançada no primeiro salto teria de estar entre
a) 4,0 m e 5,0 m.
b) 5,0 m e 6,0 m.
c) 6,0 m e 7,0 m.
d) 7,0 m e 8,0 m.
e) 8,0 m e 9,0 m.
Resolução:
Fazendo-se as considerações que:
- o alcance do segundo salto é 1,2 m menor que do primeiro salto
- o alcance do terceiro salto é 1,5 m menor que do segundo salto
- a distância alcançada no primeiro salto é x
Logo, para atingir a meta de 17,4 m, tem-se:
x + (x – 1,2) + (x – 1,2 – 1,5) = 17,4 ⇔3x = 21,3 ⇔ x = 7,1
Letra: D
7) (UNIRIO - RJ) Um grupo de amigos vai acampar num final de semana. Sabendo-se que numa certa hora da manhã de domingo, o equivalente a um terço desse grupo está envolvido com o preparo do almoço, o equivalente à metade do grupo cuida da limpeza do acampamento, o equivalente à décima parte desses dois subgrupos colhe flores nas redondezas e um elemento do grupo deleita-se com um livro de crônicas de Zuenir Ventura, quantos elementos tem esse grupo de amigos?
Resolução:
Considerando:
X - a parte do grupo envolvida com o preparo do almoço
Y - a parte do grupo que cuida da limpeza do acampamento
Z - a parte do grupo que colhe flores
V - total do grupo
Então, sabemos:
X = 1/3 V
Y = 1/2 V
Z = 1/10 (X + Y)
V = X + Y + Z + 1
(Este 1 é o elemento do grupo que está a ler)
Agora é só substituir.
V = 1/3 V + 1/2 V + 1/10 [ (1/3 V) + (1/2 V) ] + 1
V = 1/3 V + 1/2 V + 1/30 V + 1/20 V + 1 (reduzindo os termos com "V" ao mesmo denominador)
V = 20/60 V + 30/60 V + 2/60 V + 3/60 V + 1
V = 55/60 V + 1
V - 55/60V = 1 (reduzindo novamente os termos com "V" ao mesmo denominador)
60/60 V - 55/60V =1
5/60 V = 1
5 V = 60
V = 60/5
V = 12
8) Hoje, A soma das idade de um pai e um filho é 52 anos; mas há 10 anos, a idade do pai era 15 vezes a idade do filho. Determine essas idades.
9) Num campeonato de futebol, os dois melhores artilheiros pertencem ao mesmo time vencedor. Durante o campeonato, só esses dois jogadores marcaram 32 gols. Se o segundo artilheiro marcou um terço do número de gols do primeiro, quantos gols marcou cada jogador?
Resolução:
1o. jogador --> x
2o. jogador --> y
eles juntos marcaram 32, entao x+y = 32
o 2o. marcou 1/3 do 1o. , tenao y = x/3
isolando x na 2a. equaçao, fica x = 3y
volte na 1a. e troque x por 3y
3y + y = 32
4y = 32
y = 8
x = 3y
x = 3.8
x = 24
o 1o. jogador marcou 24 gols e o segundo 8 gols.
10) A quantia de R$ 2100,00 foi distribuída entre quatro pessoas do seguinte modo : a segunda recebeu metade do que recebeu a primeira; a terceira recebeu metade da soma do que recebeu a primeira com a segunda; a quarta , metade da terceira.Quanto recebeu a segunda pessoa?
Resolução:
Nesta questão, vamos chamar de x a quantia que a 2° pessoa recebeu. Agora é só você ler com calma e ir escrevendo cada uma. Como a 2° recebeu metade da 1°, então a 1° recebeu 2x. Como a 3° recebeu a metade da soma da 1° com a 2°, então ela recebeu (2x+x)/2, ou seja, 3x/2. Como a 4° recebeu metade da 3°, então recebeu 3x/4.
Resumindo:
1°: 2x
2°: x
3°: 3x/2
4°: 3x/4
A soma das quantias que cada um recebeu tem que ser 2100, certo? Então 2x+x+3x/2+3x/4=2100 -> x=400
11) Um casal tem filhos e filhas. Cada filho tem o número de irmãos igual ao número de irmãs. Cada filha tem o número de irmãos igual ao dobro do número de irmãs. Qual é o total de filhos e filhas do casal?
a) 3
b) 4
c) 5
d) 6
e) 7
12) Em uma festa de aniversário cada convidado deveria receber o mesmo número de chocolates. Três convidados mais apressados se adiantaram e o primeiro comeu 2, o segundo 3 e o terceiro 4 chocolates além dos que lhe eram devidos, resultando no consumo de metade dos chocolates da festa. Os demais chocolates foram divididos igualmente entre os demais convidados e cada um recebeu um a menos do que lhe era devido.
Quantos foram os chocolates distribuídos na festa?
a) 20
b) 24
c) 28
d) 32
e) 36
13) As pessoas A, B, C e D possuem juntas R$2.718,00. Se A tivesse o dobro do que tem, B tivesse a metade do que tem, C tivesse R$10,00 a mais do que tem e, finalmente, D tivesse R$10,00 a menos do que tem então todos teriam a mesma importância. Quanto possui cada uma das quatro pessoas?
14) (Fuvest) Os estudantes de uma classe organizaram sua festa de final de ano, devendo cada um contribuir com R$135,00 para as despesas. Como 7 alunos deixaram a escola antes da arrecadação e as despesas permaneceram as mesmas, cada um dos estudantes restantes teria de pagar R$27,00 a mais. No entanto, o diretor, para ajudar, colaborou com R$630,00. Quanto pagou cada aluno participante da festa?
a) R$136,00 b) R$138,00 c) R$140,00 d) R$142,00 e) R$144,00
15) (PUC-SP) Em um concurso os participantes devem responder a um total de 20 questões. Para cada resposta correta o candidato ganha 3 pontos e para cada resposta errada perde 2 pontos. Determine o número de acertos e erros que um candidato obteve considerando que ele totalizou 35 pontos.
11) E 12) E 13) A pessoa A possui R$ 302,00; B possui R$ 1208,00; C possui R$ 594,00 e a pessoa D, R$ 614,00. 14) E 15) 15 acertos e 5 erros 16) 200 km 17) D 18) C 19) D
20) B 21) A 22) 15
Resolução:
Considerando:
X - a parte do grupo envolvida com o preparo do almoço
Y - a parte do grupo que cuida da limpeza do acampamento
Z - a parte do grupo que colhe flores
V - total do grupo
Então, sabemos:
X = 1/3 V
Y = 1/2 V
Z = 1/10 (X + Y)
V = X + Y + Z + 1
(Este 1 é o elemento do grupo que está a ler)
Agora é só substituir.
V = 1/3 V + 1/2 V + 1/10 [ (1/3 V) + (1/2 V) ] + 1
V = 1/3 V + 1/2 V + 1/30 V + 1/20 V + 1 (reduzindo os termos com "V" ao mesmo denominador)
V = 20/60 V + 30/60 V + 2/60 V + 3/60 V + 1
V = 55/60 V + 1
V - 55/60V = 1 (reduzindo novamente os termos com "V" ao mesmo denominador)
60/60 V - 55/60V =1
5/60 V = 1
5 V = 60
V = 60/5
V = 12
8) Hoje, A soma das idade de um pai e um filho é 52 anos; mas há 10 anos, a idade do pai era 15 vezes a idade do filho. Determine essas idades.
Resolução:
Dados:
x=idade do pai
y=idade do filho
Organizando dados:
x+y=52 [equação 1]
x-10=15*(y-10) [Equação 2]
Pela equação 1, temos:
x+y=52
x=52-y
Substituindo na equação 2, temos:
(52-y)-10=15*(y-10)
52-10-y=15y-150
42+150=16y
16y=192
y=12 anos
Substituindo y por 12, na equação 1, temos:
x=52-12
x=40 anos
Resposta:
Pai=40 anos
Filho=12 anos
9) Num campeonato de futebol, os dois melhores artilheiros pertencem ao mesmo time vencedor. Durante o campeonato, só esses dois jogadores marcaram 32 gols. Se o segundo artilheiro marcou um terço do número de gols do primeiro, quantos gols marcou cada jogador?
Resolução:
1o. jogador --> x
2o. jogador --> y
eles juntos marcaram 32, entao x+y = 32
o 2o. marcou 1/3 do 1o. , tenao y = x/3
isolando x na 2a. equaçao, fica x = 3y
volte na 1a. e troque x por 3y
3y + y = 32
4y = 32
y = 8
x = 3y
x = 3.8
x = 24
o 1o. jogador marcou 24 gols e o segundo 8 gols.
10) A quantia de R$ 2100,00 foi distribuída entre quatro pessoas do seguinte modo : a segunda recebeu metade do que recebeu a primeira; a terceira recebeu metade da soma do que recebeu a primeira com a segunda; a quarta , metade da terceira.Quanto recebeu a segunda pessoa?
Resolução:
Nesta questão, vamos chamar de x a quantia que a 2° pessoa recebeu. Agora é só você ler com calma e ir escrevendo cada uma. Como a 2° recebeu metade da 1°, então a 1° recebeu 2x. Como a 3° recebeu a metade da soma da 1° com a 2°, então ela recebeu (2x+x)/2, ou seja, 3x/2. Como a 4° recebeu metade da 3°, então recebeu 3x/4.
Resumindo:
1°: 2x
2°: x
3°: 3x/2
4°: 3x/4
A soma das quantias que cada um recebeu tem que ser 2100, certo? Então 2x+x+3x/2+3x/4=2100 -> x=400
a) 3
b) 4
c) 5
d) 6
e) 7
12) Em uma festa de aniversário cada convidado deveria receber o mesmo número de chocolates. Três convidados mais apressados se adiantaram e o primeiro comeu 2, o segundo 3 e o terceiro 4 chocolates além dos que lhe eram devidos, resultando no consumo de metade dos chocolates da festa. Os demais chocolates foram divididos igualmente entre os demais convidados e cada um recebeu um a menos do que lhe era devido.
Quantos foram os chocolates distribuídos na festa?
a) 20
b) 24
c) 28
d) 32
e) 36
13) As pessoas A, B, C e D possuem juntas R$2.718,00. Se A tivesse o dobro do que tem, B tivesse a metade do que tem, C tivesse R$10,00 a mais do que tem e, finalmente, D tivesse R$10,00 a menos do que tem então todos teriam a mesma importância. Quanto possui cada uma das quatro pessoas?
14) (Fuvest) Os estudantes de uma classe organizaram sua festa de final de ano, devendo cada um contribuir com R$135,00 para as despesas. Como 7 alunos deixaram a escola antes da arrecadação e as despesas permaneceram as mesmas, cada um dos estudantes restantes teria de pagar R$27,00 a mais. No entanto, o diretor, para ajudar, colaborou com R$630,00. Quanto pagou cada aluno participante da festa?
a) R$136,00 b) R$138,00 c) R$140,00 d) R$142,00 e) R$144,00
15) (PUC-SP) Em um concurso os participantes devem responder a um total de 20 questões. Para cada resposta correta o candidato ganha 3 pontos e para cada resposta errada perde 2 pontos. Determine o número de acertos e erros que um candidato obteve considerando que ele totalizou 35 pontos.
16) Ao alugar um carro por um dia, Marcos fez o seguinte contrato: R$ 50,00 a diária mais R$ 0,50 por km. Ao entregar o carro Marcos pagou R$ 150,00. Quantos km ele andou?
17) (CESD-2008) Ao distribuir R$ 80,00 entre duas meninas, de modo que a mais nova receba R$ 16,00 a menos que a mais velha, a quantia dada à mais velha será um valor múltiplo de R$
a) 9,00.
b) 7,00.
c) 5,00.
d) 4,00.
18) Três amigos M, N e P têm juntos R$ 1.054,00. Se M tivesse o dobro do que tem, N tivesse a metade do que tem e P tivesse R$ 10,00 a mais do que tem, então todos teriam a mesma importância. Quantos reais possui N?
a) 152
b) 294
c) 608
d) 304
19) A idade de uma pessoa é hoje o triplo da idade da outra e daqui a 11 anos será o dobro. A soma de suas idades atuais é:
a) 18
b) 36
c) 48
d) 44
20) Para cercar um terreno retangular de 50 m de comprimento, será feita uma porteira de madeira de 3m de extensão e uma cerca com 5 fios de arame. Se a medida da largura desse terreno é igual a dois quintos da do comprimento, então o número de metros de arame necessário será:
a) 700.
b) 685.
c) 557.
d) 535.
21) Uma pasto retangular de 79,15 m de comprimento e de 4125 cm de largura será cercado com 3 voltas de arame. Se cada rolo de arame tem 120,4 m, então serão necessários ________ rolos.
a) 6
b) 12
c) 9
d) 5
22) O triplo de um número, diminuído de 12, é igual a 33. Qual é esse número?
Gabarito:17) (CESD-2008) Ao distribuir R$ 80,00 entre duas meninas, de modo que a mais nova receba R$ 16,00 a menos que a mais velha, a quantia dada à mais velha será um valor múltiplo de R$
a) 9,00.
b) 7,00.
c) 5,00.
d) 4,00.
18) Três amigos M, N e P têm juntos R$ 1.054,00. Se M tivesse o dobro do que tem, N tivesse a metade do que tem e P tivesse R$ 10,00 a mais do que tem, então todos teriam a mesma importância. Quantos reais possui N?
a) 152
b) 294
c) 608
d) 304
19) A idade de uma pessoa é hoje o triplo da idade da outra e daqui a 11 anos será o dobro. A soma de suas idades atuais é:
a) 18
b) 36
c) 48
d) 44
20) Para cercar um terreno retangular de 50 m de comprimento, será feita uma porteira de madeira de 3m de extensão e uma cerca com 5 fios de arame. Se a medida da largura desse terreno é igual a dois quintos da do comprimento, então o número de metros de arame necessário será:
a) 700.
b) 685.
c) 557.
d) 535.
21) Uma pasto retangular de 79,15 m de comprimento e de 4125 cm de largura será cercado com 3 voltas de arame. Se cada rolo de arame tem 120,4 m, então serão necessários ________ rolos.
a) 6
b) 12
c) 9
d) 5
22) O triplo de um número, diminuído de 12, é igual a 33. Qual é esse número?
11) E 12) E 13) A pessoa A possui R$ 302,00; B possui R$ 1208,00; C possui R$ 594,00 e a pessoa D, R$ 614,00. 14) E 15) 15 acertos e 5 erros 16) 200 km 17) D 18) C 19) D
20) B 21) A 22) 15
Nenhum comentário:
Postar um comentário