Relações métricas em um triângulo retângulo
O triângulo é o polígono com menor número de lados, mas é uma das formas geométricas mais importantes no estudo da geometria. Sempre intrigou matemáticos desde a Antiguidade. Triângulo retângulo é aquele que apresenta um ângulo interno medindo 90o. Esse tipo de triângulo apresenta propriedades e características muito relevantes. Faremos o estudo das relações entre as medidas dos lados do triângulo retângulo.
Todo triângulo retângulo é composto por dois catetos e uma hipotenusa. A hipotenusa é o maior lado do triângulo retângulo e está oposto ao ângulo reto.
Observe a figura abaixo.
Todo triângulo retângulo é composto por dois catetos e uma hipotenusa. A hipotenusa é o maior lado do triângulo retângulo e está oposto ao ângulo reto.
Observe a figura abaixo.
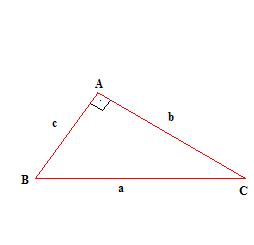
Temos que:
a → é a hipotenusa
b e c → são os catetos.
A perpendicular a BC, traçada por A, é a altura h, relativa à hipotenusa do triângulo.
a → é a hipotenusa
b e c → são os catetos.
A perpendicular a BC, traçada por A, é a altura h, relativa à hipotenusa do triângulo.
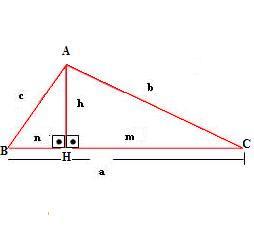
BH = n e CH = m são as projeções dos catetos sobre a hipotenusa.
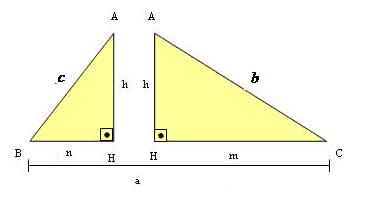
Os três triângulos são semelhantes
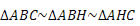
Da semelhança de triângulos obtemos as seguintes relações:
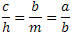
Daí segue que:
b2 = am e ah = bc
Temos, também, as seguintes relações:
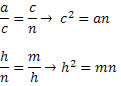
E a mais famosa das relações métricas no triângulo retângulo:
a2 = b2 + c2
Que é o teorema de Pitágoras.
Observe que temos cinco relações métricas no triângulo retângulo:
1. b2 = am
2. ah = bc
3. c2 = an
4. h2 = mn
5. a2 = b2 + c2
Todas elas são de grande utilidade na resolução de problemas que envolvem triângulos retângulos.
Exemplo. Determine as medidas da altura relativa à hipotenusa e dos dois catetos do triângulo abaixo.
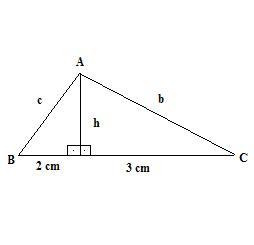
Solução: Temos que
n = 2 cm
m = 3 cm
Utilizando a quarta relação descrita anteriormente, obtemos:
h2 = mn
h2 = 3∙2
h2 = 6
h = √6
n = 2 cm
m = 3 cm
Utilizando a quarta relação descrita anteriormente, obtemos:
h2 = mn
h2 = 3∙2
h2 = 6
h = √6
Segue que:
a = 2 + 3 = 5 cm
Daí, utilizando a primeira relação, obtemos:
b2 = am
b2 = 5∙3
b2 = 15
b = √15
Da terceira relação, obtemos:
c2 = an
c2 = 5∙2
c2 = 10
c = √10
a = 2 + 3 = 5 cm
Daí, utilizando a primeira relação, obtemos:
b2 = am
b2 = 5∙3
b2 = 15
b = √15
Da terceira relação, obtemos:
c2 = an
c2 = 5∙2
c2 = 10
c = √10
Razões trigonométricas
Observe a figura abaixo que representa um triângulo retângulo.
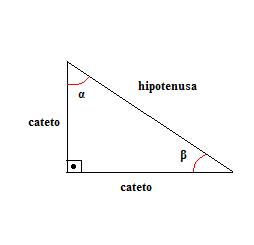
Note que o maior lado é denominado de hipotenusa e os outros dois lados de catetos. A hipotenusa é o lado que fica oposto ao ângulo reto (ângulo de 90o). Além do ângulo reto, há dois ângulos agudos, α e β. A trigonometria estabelece relações entre os ângulos agudos do triângulo retângulo e as medidas de seus lados. Vejamos quais são essas relações.
O seno de um ângulo no triângulo retângulo é a razão entre o cateto oposto e a hipotenusa.
O seno de um ângulo no triângulo retângulo é a razão entre o cateto oposto e a hipotenusa.
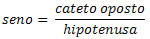
O cosseno de um ângulo no triângulo retângulo é a razão entre o cateto adjacente e a hipotenusa.
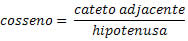
A tangente de um ângulo no triângulo retângulo é a razão entre o cateto oposto e o cateto adjacente.
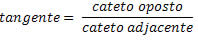
Definidas as razões trigonométricas, obtemos as seguintes igualdades para o triângulo retângulo abaixo:
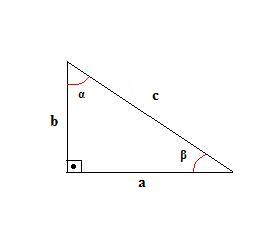

Exemplo 1 Determine os valores de seno, cosseno e tangente dos ângulos agudos do triângulo abaixo.
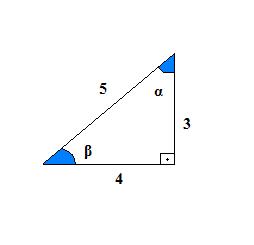
Solução: Temos que
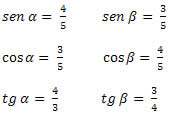
Exemplo 2. Sabendo que sen α =1/2 , determine o valor de x no triângulo retângulo abaixo:
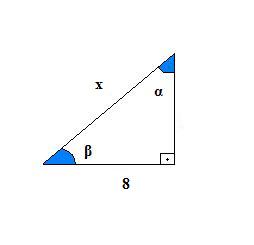
Solução: A hipotenusa do triângulo é x e o lado com medida conhecida é o cateto oposto ao ângulo α. Assim, temos que:
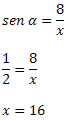
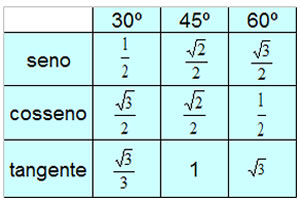
Tabela de Razões Trigonométricas
Os cálculos envolvendo as relações trigonométricas, ao serem efetuados, necessitam de alguns valores de ângulos, que estão presentes na seguinte tabela de razões trigonométricas:
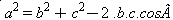
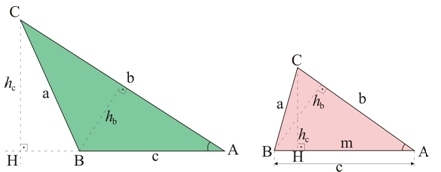
Em qualquer triângulo quando um lado é igual à soma dos quadrados dos outros dois, menos duas vezes o produto desses dois lados pelo cosseno do ângulo formado por eles.
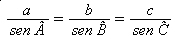
Os cálculos envolvendo as relações trigonométricas, ao serem efetuados, necessitam de alguns valores de ângulos, que estão presentes na seguinte tabela de razões trigonométricas:

Lei dos Cossenos
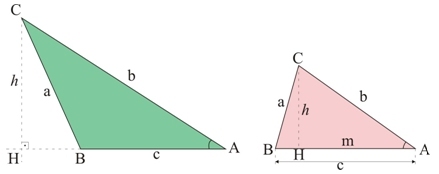
Considere um triângulo ABC qualquer de lados a, b e c:

Para esses triângulos podemos escrever:
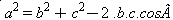
Lei dos Senos
A lei dos senos estabelece a relação entra a mediada de um lado e o seno do ângulo oposto a esse lado. Para um triângulo ABC de lados a, b, c, podemos escrever.
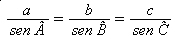

A lei dos senos determina que a razão entre a medida de um lado e o seno do ângulo oposto é constante em um mesmo triângulo.
Fontes: www.infoescola.com
www.brasilescola.com
www.alunosonline.com.br
Questões sobre relações métricas e razões trigonométricas no triângulo retângulo
1) (UF – PI) Um avião decola, percorrendo uma trajetória retilínea, formando com o solo, um ângulo de 30º (suponha que a região sobrevoada pelo avião seja plana). Depois de percorrer 1 000 metros, qual a altura atingida pelo avião?
Solução:
.gif)
A altura será de 500 metros.
2) A rua Tenório Quadros e a avenida Teófilo Silva, ambas retilíneas, cruzam-se conforme um ângulo de 30º. O posto de gasolina Estrela do Sul encontra-se na avenida Teófilo Silva a 4 000 m do citado cruzamento. Portanto, determine em quilômetros, a distância entre o posto de gasolina Estrela do Sul e a rua Tenório Quadros?
Solução:
.gif)
.gif)
3) (Unisinos – RS) Um avião levanta voo sob um ângulo constante de 20º. Após percorrer 2 000 metros em linha reta, qual será a altura atingida pelo avião, aproximadamente? (Utilize: sem 20º = 0,342; cos 20º = 0,94 e tg 20º = 0,364).
Solução:
.gif)
.gif)
4) (Unifor–CE) Sabe-se que em todo triângulo a medida de cada lado é diretamente proporcional ao seno do ângulo oposto ao lado. Usando essa informação, determine a medida do lado AB do triângulo representado:
.gif)
5) (FEI-SP) Se em um triângulo ABC o lado AB mede 3 cm, o lado BC mede 4 cm e o ângulo interno formado entre os lados AB e BC medem 60º, determine a medida do lado AC.
Solução:
.gif)
6) Calcule o valor da medida x no triângulo representado pela seguinte figura:
.gif)
Solução:
.gif)
7) (PUC-MG) Na figura, AB = 5dm, AD = 5√7 dm, DBC = 60º e DCA = 90º. Determine a medida de CD em decímetros.
.gif)
Solução:
.gif)
8) Em um triangulo retângulo, sua altura(h) é = 5 e sua hipotenusa(a) é =26. Calcule o cateto b (cateto maior).
Vamos recordar as relações métricas em um triângulo retângulo:
a = m + n
b² = a.m
c² = a.n
b.c = a.h
h² = m.n
a² = b² + c²
no exercício dado, sabemos que
h = 5
a = 26
observe que nenhuma das relações métricas envolve apenas essas duas medidas
vamos ter que encontrar um caminho.
Façamos, primeiro:
m + n = a
m + n = 26
n = 26 - m (I)
b² = a . m (onde m é a maior das projeções)
b² = 26m (II)
c² = a.n
c² = 26n --> c² = 26(26 - m) --> c² = 676 - 26m (III)
b . c = a . h
b . c = 26 . 5
b . c = 130
eleva ao quadrado:
b² c² = 16900
substitui (II) e (III)
26m ( 676 - 26m) = 16900
17576m - 676m² = 16900
676m² - 17576m + 16900 = 0 --> simplifica por 676
m² - 26m + 25 = 0
resolve por báskara ou pela soma e produto:
m' = 25
m" = 1 (despreza por ser o menor)
b² = 26m (II)
b² = 25 . 26 ==> b = 5√26 m que é o cateto maior
como a = m + n
n = 1
c² = 26n --> c² = 26 --> c= √26 m que é o cateto menor
Poderíamos também usar outras duas relações métricas:
h = m.n ---> m . n = 25 (I)
a = m + n --> m + n = 26 donde m = 26 - n (II)
Substitui (II) em (I)
( 26 - n ) . n = 25
n² - 26n + 25 = 0
resolvendo por báskara ou pela soma e produto:
n' = 1
n" = 25 (despreza, pois consideramos inicialmente que m é a maior)
como
m = 26 - n (II)
m = 26 - 1
m = 25
assim, sabendo que
b² = a.m
temos
b² = 26 . 25
b = √ 5² . 26
b = 5 √ 26
logo, o cateto maior b = 5 √26 m
a = m + n
b² = a.m
c² = a.n
b.c = a.h
h² = m.n
a² = b² + c²
no exercício dado, sabemos que
h = 5
a = 26
observe que nenhuma das relações métricas envolve apenas essas duas medidas
vamos ter que encontrar um caminho.
Façamos, primeiro:
m + n = a
m + n = 26
n = 26 - m (I)
b² = a . m (onde m é a maior das projeções)
b² = 26m (II)
c² = a.n
c² = 26n --> c² = 26(26 - m) --> c² = 676 - 26m (III)
b . c = a . h
b . c = 26 . 5
b . c = 130
eleva ao quadrado:
b² c² = 16900
substitui (II) e (III)
26m ( 676 - 26m) = 16900
17576m - 676m² = 16900
676m² - 17576m + 16900 = 0 --> simplifica por 676
m² - 26m + 25 = 0
resolve por báskara ou pela soma e produto:
m' = 25
m" = 1 (despreza por ser o menor)
b² = 26m (II)
b² = 25 . 26 ==> b = 5√26 m que é o cateto maior
como a = m + n
n = 1
c² = 26n --> c² = 26 --> c= √26 m que é o cateto menor
Poderíamos também usar outras duas relações métricas:
h = m.n ---> m . n = 25 (I)
a = m + n --> m + n = 26 donde m = 26 - n (II)
Substitui (II) em (I)
( 26 - n ) . n = 25
n² - 26n + 25 = 0
resolvendo por báskara ou pela soma e produto:
n' = 1
n" = 25 (despreza, pois consideramos inicialmente que m é a maior)
como
m = 26 - n (II)
m = 26 - 1
m = 25
assim, sabendo que
b² = a.m
temos
b² = 26 . 25
b = √ 5² . 26
b = 5 √ 26
logo, o cateto maior b = 5 √26 m
9) No triângulo retângulo abaixo determinar a hipotenusa, as projeções dos catetos sobre a hipotenusa e a altura relativa a hipotenusa:
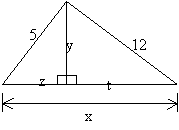
Resolução:
Pelo teorema de Pitágoras temos:
x2 = 52 + 122
x2 = 169
x = 13
Aplicando as relações de projeções de catetos, vem:
52 = x . z
13 . z = 25
z = 25 / 13
122 = x . t
13 . t = 144
t = 144 / 13
Aplicando a relação do produto dos catetos, vem:
x . y = 5 . 12
13 . y = 60
y = 60 / 13
10) Dado o triângulo retângulo ABC, reto em A, representado na figura abaixo, calcule os valores desconhecidos (x, m, n e h).
x = 4 m,
h = 12/5 m = 2,4 m,
m = 9/5 m = 1,8 m,
n = 16/5 m =3,2 m
h = 12/5 m = 2,4 m,
m = 9/5 m = 1,8 m,
n = 16/5 m =3,2 m
11) Se cada ângulo de um triângulo equilátero mede 60 º, calcule a medida da altura de um triângulo equilátero de lado 20 cm.
12) Calcular os catetos de um triângulo retângulo cuja hipotenusa mede 6 cm e um dos ângulos mede 60º.
13) Encontre x e y:
a) 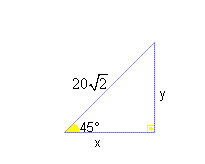 b)
b) 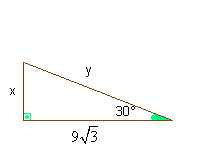
14) Encontre a medida RA sabendo que tg  = 3.
15) (MAPOFEI) Na figura abaixo, AB = 4 cm, Â = 30º e ângulo C = 45°. Calcular BH.
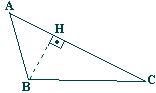
16) Um alpinista deseja calcular a altura de uma encosta que vai escalar. Para isso, afasta-se, horizontalmente, 80 m do pé da encosta e visualiza o topo sob um ângulo de 55º com o plano horizontal. Calcule a altura da encosta. (Dados: sem 55º = 0,81, cos 55º = 0,57 e tg 55º = 1,42).
17) Uma escada encostada em um edifício tem seus pés afastados a 50 m do edifício, formando assim, com o plano horizontal, um ângulo de 32º. A altura do edifício é aproximadamente: (sen 32º = 05299, cos 32′ = 0,8480 e tg 32º = 0,6249)
18) (Cesgranrio-RJ) Num triângulo retângulo em A, a altura relativa à hipotenusa mede 12, e o menor dos segmentos que ela determina sobre a hipotenusa, 9. O menor lado do triângulo mede:
 a)
a) ![clip_image002[4] clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgi6iG1uBjhKEPqg1-2HyIv-OwDs66voxKw-q-KVAhgzoNzdlNP20PndYnaUsyYqnbO0SEtujbFDZ_bWQc3236-Bq630006c5STbuzv9m5j69gdGbmLtqhZuSuXxnF1yn5JhTFt9kqcXJY/?imgmax=800) b)
b) ![clip_image002[6] clip_image002[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhU6CuZeYX9TlEivBnSy967ldXQi8p0kBlvQDyigsTTzg6ET_Fw5efGFUB-wgQuTipsOBhIFgQ9q7-JyXH6ZqJcqULbt1KoIDkD6b8uRRB8Sf1QtcE17PhsOZPeYNi5JNRxSoPLXL55lhI/?imgmax=800) c)
c) ![clip_image002[8] clip_image002[8]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiiySuBFE9l5OUr-3tGbMnUaESCAlQUXAcdfLOuyBY1rqimdCaBfgAEZmqIM281F1_tNiKYTakaNxab5dw8SHzIFGfh4O2tOxLSnkUaUd17Za590LE795cPbHqP5aexzBOOSEHAwVzQAm8/?imgmax=800) d) ½ e) 4
d) ½ e) 4
a) 12,5 b) 13 c) 15 d) 16 e) 16,5
19) (FATEC-SP) Se os catetos de um triângulo retângulo T, medem, respectivamente, 12 cm e 5 cm, então a altura de T relativa à hipotenusa é:
a) 12/5 m b) 5/13 m c) 12/13 m d) 25/13 m e) 60/13 m
20) Dado o triângulo retângulo ABC, reto em A, representado na figura abaixo, calcule os valores desconhecidos (x, m, n e h).
21) O valor de y no triângulo abaixo é:
 a)
a)
Gabarito:
11) 10√3 12) 3√3 e 3 13) y = 3,78 e x = 8,19 14) a) x = 20 e y = 20 b) x = 9 e y = 18
15) tg  = 1 e tg Ê = 1 16) 2 cm 14) 113,6 m 17) 31,24 m 18) C 19) E 20) x = 4 m, h = 12/5 m = 2,4 m, m = 9/5 m = 1,8 m, n = 16/5 m =3,2 m 21) C

parabéns para o professor que preparou esse material que é um bom resumo para quem quer estufar e tirar suas dúvidas.
ResponderExcluirvery good,I learned everything about sin
ResponderExcluir