questões vestibular equações trigonométricas

1. Introdução

Chamamos de Equação Trigonométrica a qualquer na qual a incógnita faz parte do arco de alguma função trigonométrica.
São exemplos de equações trigonométricas:
5 sen x + 3 cos x = 2
tg = cotg x

Assim, por exemplo, na equação cos x 1/2 temos que π/3 rad é uma solução, pois cos π/3 = 1/2.
No entanto, em R, existem infinitas soluções para a equação acima!
Todos os arcos cujas medidas são da forma x = π/3 + k*2π ou da forma x = -π/3 + k*2π, com k E Z, também constituem solução, pois para todos eles, o cosseno vale 1/2. O conjunto solução é, portanto:
S = { x E R / x = ± π/3 + k*2π, k E Z}

Esse fato sugere a lembrança de que a função cosseno não é injetora, pois para mais de um valor de x obtemos a mesma imagem y = cos x. Então, a função cosseno definida de R em R,não tem inversa.

Não existe um método único para resolver todoas as equações trigonométricas. No entanto, a maioria delas pode ser transformada em outras mais simples, porém equivalentes, ou seja, de mesma solução.
Na verdade, uma grande parte delas pode ser resolvida se soubermos resolver as seguintes equações fundamentais:

a) sen x = sen a
b) cos x = cos a
c) tg x = tg a                        (a E R)

Vejamos separadamente cada uma delas.

2. Equação do tipo sen x = sen a

 Ela baseia-se no fato de que, se dois arcos têm o mesmo seno, então eles são côngruos ou suplementares.



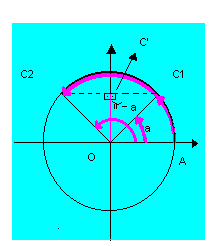
Portanto, a solução genérica de uma equação do tipo sen x = sen a, será:

 x = π - a + k*2π com k E Z ou x = 2kπ + a.

Exemplo:

seja a equação elementar sen x = 0,5.

Como 0,5 = sen 30º = sen p/6, vem, utilizando o resultado geral obtido acima:
sen x = sen p/6, de onde conclui-se:
x = (2k + 1).p - p/6  ou  x = 2kp + p/6, com k inteiro, que representa a solução genérica da equação dada. Fazendo k variar no conjunto dos números inteiros, obteremos as soluções particulares da equação.
Assim, por exemplo, fazendo k = 0, obteremos por mera substituição na solução genérica encontrada acima,
x = - p/6 ou x = p/6; fazendo k = 1, obteremos
x = 17p/6 ou x = 13p/6, e assim sucessivamente. Observe que a equação dada, possui um número infinito de soluções em R – conjunto dos números reais.

Poderemos escrever o conjunto solução da equação dada na forma geral: S = {x| x Î R;  x =(2k + 1)p - p/6 ou x = 2kp + p/6, k Î Z}

3. Equação do tipo cos x = cos a

a solução genérica de uma equação do tipo cos x = cos a, será dada por:
x = ± a + 2kp com k E Z

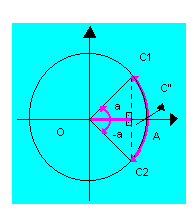
Exemplo: 

3*cos x = 0 ► cos x = 0. Então π/2 rad é uma solução, pois cos π/2 = 0.

Assim, temos: cos x = cos π/2 

O conjunto solução é:

S = {x E R/ x =  ± π/2 + 2kπ, K E Z} ou S = {x = π/2 + kπ, k E Z}.

4. Equação do tipo tg x = tg a

Ela baseia-se no fato de que, se dois arcos têm a mesma tangente, então eles são côngruos ou têm suas  extremidades simétricas em relação  ao centro do ciclo trigonométrico.

 

A solução genérica de uma equação do tipo tg x = tg a , será dada por x = kπ + a  com k E Z.

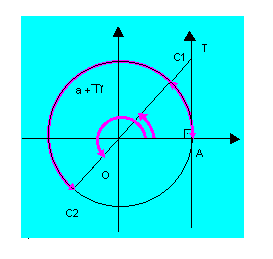
Exemplos:

Resolva a equação tg x=1

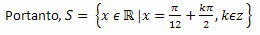
Solução: Sabemos que um arco que possui a tangente igual a 1 é o arco de 45^o ou π/4



 

Exercícios resolvidos

1) Resolver a equação 2*sen(3x) + 1 = 0

Resolução: 

Temos que 2*sen(3x) + 1 = 0 

Uma solução é 3x = 7π/6 rad, pois sen 7π/6 = - 1/2. Assim, temos: sen 3x = sen 7π/6

Entao: 3x = 7π/6 + 2kπ ou 3x = - π/6 + 2kπ , k E R.

              x = 7π/18 + 2kπ/3 ou x = - π/18 + 2kπ/3

Concluímos que o conjunto solução é:

S = {x E R/x = 7π/18 + 2kπ/3 ou x = - π/18 + 2kπ/3, k E Z}

2) Encontre a solução da equação cos x + 1 = 0

Resolução:

Temos que cos x = - 1. Então x = πrad é uma solução, pois cos π = -1.

Assim, cos x = cos π

Como os arcos de medidas πrad e - πrad possuem a mesma extremidade, o conjunto solução é:

S = {x E R/x = π + 2kπ, k E Z}

3) Encontre a solução da equação tg x = √3

Resolução:
Uma solução é x = π/3 rad, pois tg π/3 = sen π/3 / cos π//3 = √3/2 / 1/2 = √3
Assim sendo, o conjunto solução é:
S = {x E R/x = π/3 + kπ, k E Z}

4) Ache o o conjunto solução da equação sen (5x) + sen (2x) = 0

Resolução:

Observe que é possível transformar o 1º membro em um produto; além disso, o 2º membro é zero. Assim sendo, lembrando que sen p + sen q = 2*sen p + q / 2* cos p - q / 2, temos:

2*sen 5x + 2x /2*cos 5x - 2x /2 = 0 ► sen 7x / 2*cos3x /2 = 0 ► sen 7x/ 2 = 0 ou cos 3x /2 = 0

Para sen 7x/ 2 = sen 0, temos: 7x/ 2 = kπ, k E Z. Portanto:  7x = 2kπ ► x = 2kπ / 7, k E Z

Para cos 3x/ 2 = cos π/2, temos: 3x / 2 = π/ 2 + kπ, k E Z.

Entao: 3x = π + 2kπ ► x =  π/ 3 + 2kπ/ 3, k E Z.

O conjunto solução é: S = {x E R/ x = π/3 + 2kπ/ 3 ou x = 2kπ/ 7, k E Z}

Obs: esse mesmo problema poderia ser resolvido assim:

sen (5x) + sen (2x) = 0  ► sen (5x) = - sen (2x) 

como: - sen (2x) = sen (- 2x)  desse modo temos:

5x = - 2x + 2kπ ou 5x = π - (-2x) + 2kπ, k E Z, daí obtemos:

x = 2kπ/ 7 ou x = π/ 3 + 2kπ/ 3, k E Z